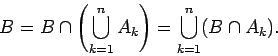Επόμενο: Ανεξαρτησία γεγονότων Επάνω: p1 Προηγούμενο: Δεσμευμένη Πιθανότητα
Στενά συνδεδεμένα με την έννοια της δεσμευμένης πιθανότητας είναι το Θεώρημα Ολικής Πιθανότητας.
Υποθέτουμε ότι
![]() είναι
είναι ![]() ξένα
ανά δύο ενδεχόμενα των οποίων η ένωση ισούται με το
ξένα
ανά δύο ενδεχόμενα των οποίων η ένωση ισούται με το ![]() ,
είναι δηλαδή μια
διαμέριση, όπως λέγεται, του
,
είναι δηλαδή μια
διαμέριση, όπως λέγεται, του ![]() . Υποθέτουμε επίσης
ότι είναι γνωστές οι πιθανότητες
. Υποθέτουμε επίσης
ότι είναι γνωστές οι πιθανότητες ![]() και
και ![]() για
για
![]() . Τότε αν Β είναι ένα ενδεχόμενο
του
. Τότε αν Β είναι ένα ενδεχόμενο
του ![]() , ποια είναι η
, ποια είναι η ![]() ; Για να λύσουμε αυτό το
πρόβλημα παρατηρούμε ότι αφού τα
; Για να λύσουμε αυτό το
πρόβλημα παρατηρούμε ότι αφού τα ![]() είναι μια διαμέριση του
είναι μια διαμέριση του ![]() ,
θα είναι
,
θα είναι