Επόμενο: Άλλες Ιδιότητες της Πιθανότητας Επάνω: p1 Προηγούμενο: Στοιχεία από τη Θεωρία
Υπάρχουν δύο αξιοσημείωτες μέθοδοι για τον ορισμό
(ουσιαστικά την εκτίμηση) της πιθανότητας
ενός γεγονότος. Θα τους παρουσιάσουμε ξεκινώντας με ένα
παράδειγμα.
Στο πείραμα τύχης της ρίψης ενός ζαριού, ο ΔΧ είναι το σύνολο
των αριθμών
![]() .
Αν ορίσουμε με
.
Αν ορίσουμε με ![]() το γεγονός ``το αποτέλεσμα του πειράματος να
είναι αριθμός άρτιος'', τότε το γεγονός
το γεγονός ``το αποτέλεσμα του πειράματος να
είναι αριθμός άρτιος'', τότε το γεγονός ![]() θα περιλαμβάνει τα
σημεία
θα περιλαμβάνει τα
σημεία ![]() .
.
Έστω ότι επαναλαμβάνουμε το πείραμα ρίψης ζαριού ![]() φορές,
και συμβολίζουμε με
φορές,
και συμβολίζουμε με ![]() το πλήθος εκείνων από τις
το πλήθος εκείνων από τις ![]() δοκιμές στις οποίες το αποτέλεσμα της ρίψης ήταν 1, με
δοκιμές στις οποίες το αποτέλεσμα της ρίψης ήταν 1, με
![]() το πλήθος εκείνων όπου το αποτέλεσμα ήταν 2, κ.ο.κ.
το πλήθος εκείνων όπου το αποτέλεσμα ήταν 2, κ.ο.κ.
Το ποσοστό των εμφανίσεων των αποτελεσμάτων 1, 2, ..., 6,
είναι λοιπόν
Δεδομένου ότι το γεγονός ![]() περιλαμβάνει τα σημεία
περιλαμβάνει τα σημεία ![]() ,
μπορεί να γίνει εύκολα αντιληπτό
ότι η σχετική συχνότητα του γεγονότος
,
μπορεί να γίνει εύκολα αντιληπτό
ότι η σχετική συχνότητα του γεγονότος ![]() θα είναι το άθροισμα
θα είναι το άθροισμα
Ο απλούστερος ορισμός της πιθανότητας ![]() είναι ο γνωστός ως
κλασσικός
ορισμός, και έχει τις ρίζες του στα τυχερά παιχνίδια.
Σύμφωνα με αυτόν, η πιθανότητα ενός γεγονότος
είναι ο γνωστός ως
κλασσικός
ορισμός, και έχει τις ρίζες του στα τυχερά παιχνίδια.
Σύμφωνα με αυτόν, η πιθανότητα ενός γεγονότος ![]() ορίζεται ως
ορίζεται ως
![]() = (πλήθος σημείων του γεγονότος
= (πλήθος σημείων του γεγονότος ![]() )/
(πλήθος σημείων του
)/
(πλήθος σημείων του ![]() ).
).
Περιφραστικά, η πιθανότητα ενός γεγονότος ![]() είναι το πηλίκο
των διαφόρων τρόπων με τους οποίους μπορεί να πραγματοποιηθεί το
είναι το πηλίκο
των διαφόρων τρόπων με τους οποίους μπορεί να πραγματοποιηθεί το ![]() (των "ευνοικών" περιπτώσεων για το
(των "ευνοικών" περιπτώσεων για το ![]() ) δια του πλήθους
των δειγματοσημείων του
) δια του πλήθους
των δειγματοσημείων του ![]() .
.
Για να ισχύει όμως ο κλασσικός ορισμός, θα πρέπει να υπάρχουν οι εξής προυποθέσεις:
Ο κλασσικός ορισμός της πιθανότητας παρουσιάζει αδυναμίες.
Κατ' αρχήν χρησιμοποιεί εκφράσεις όπως ``ίδιες δυνατότητες''
ή ``ίδιες ευκαιρίες'', οι οποίες δεν μπορούν να ορισθούν επαρκώς
από μαθηματικής πλευράς, αλλά επαφίενται στη διαίσθηση.
Επίσης, συχνά εμφανίζονται στην πράξη δειγματοχώροι ![]() με άπειρο πλήθος στοιχείων, οπότε η προυπόθεση (1) δεν συντρέχει.
με άπειρο πλήθος στοιχείων, οπότε η προυπόθεση (1) δεν συντρέχει.
Υπάρχουν δύο εξίσου πιθανά αποτελέσματα, Κ και Γ, και επειδή το ευνοικό αποτέλεσμα είναι ένα από αυτά (Κ), συμπεραίνουμε ότι η πιθανότητα να έρθει Κ σε μιά ρίψη είναι 1/2 .
Εδώ ![]() ={ΚΚ,ΚΓ,ΓΚ,ΓΓ}, ενώ το σύνολο που αντιστοιχεί
στο γεγονός που περιγράφηκε είναι το {ΚΓ}, οπότε
={ΚΚ,ΚΓ,ΓΚ,ΓΓ}, ενώ το σύνολο που αντιστοιχεί
στο γεγονός που περιγράφηκε είναι το {ΚΓ}, οπότε ![]() (ΚΓ)=1/4.
(ΚΓ)=1/4.
Ο ΔΧ του προβλήματος είναι ο ![]() =
=
![]() .
Έστω
.
Έστω ![]() και
και ![]() τα ενδεχόμενα ``να έρθει 4'' και ``να έρθει άρτιος'',
αντίστοιχα. Τότε
τα ενδεχόμενα ``να έρθει 4'' και ``να έρθει άρτιος'',
αντίστοιχα. Τότε ![]() και
και
![]() , οπότε
, οπότε
![]() και
και
![]() .
.
Ένας άλλος ορισμός της πιθανότητας ο οποίος δεν θέτει περιορισμούς
στον ΔΧ ![]() είναι εκείνος που βασίζεται στην έννοια της σχετικής
συχνότητας, και ο οποίος βασίζεται σε πολλές επαναλήψεις
ενός δεδομένου πειράματος τύχης.
Θεωρήστε έναν οποιονδήποτε δειγματοχώρο
είναι εκείνος που βασίζεται στην έννοια της σχετικής
συχνότητας, και ο οποίος βασίζεται σε πολλές επαναλήψεις
ενός δεδομένου πειράματος τύχης.
Θεωρήστε έναν οποιονδήποτε δειγματοχώρο ![]() ο οποίος
αναφέρεται σε ένα συγκεκριμένο πείραμα τύχης, και έστω
ο οποίος
αναφέρεται σε ένα συγκεκριμένο πείραμα τύχης, και έστω ![]() ένα γεγονός.
Το εν λόγω πείραμα τύχης επαναλαμβάνεται
ένα γεγονός.
Το εν λόγω πείραμα τύχης επαναλαμβάνεται ![]() φορές, και έστω
φορές, και έστω
![]() ο αριθμός των φορών που πραγματοποιείται το γεγονός
ο αριθμός των φορών που πραγματοποιείται το γεγονός ![]() .
Ο αριθμός
.
Ο αριθμός ![]() λέγεται συχνότητα του Α, και το πηλίκο
λέγεται συχνότητα του Α, και το πηλίκο
![]() σχετική συχνότητα του
σχετική συχνότητα του ![]() .
.
Θεωρούμε την ακολουθία των σχετικών συχνοτήτων του ![]() ,
,
![]() , με
, με ![]() , και υποθέτουμε ότι καθώς
, και υποθέτουμε ότι καθώς
![]() υπάρχει το όριο
υπάρχει το όριο
![]() . Το όριο αυτό
ορίζεται ως η πιθανότητα του
. Το όριο αυτό
ορίζεται ως η πιθανότητα του ![]() ,
, ![]() . Ο ορισμός αυτός είναι
γνωστός ως στατιστικός ορισμός, και ικανοποιεί την αντίληψη
που διαισθητικά έχει κανείς για την έννοια της πιθανότητας.
. Ο ορισμός αυτός είναι
γνωστός ως στατιστικός ορισμός, και ικανοποιεί την αντίληψη
που διαισθητικά έχει κανείς για την έννοια της πιθανότητας.
Αδυναμίες παρουσιάζει και αυτός ο ορισμός, που σχετίζονται
με την απαίτηση του πολύ μεγάλου ![]() . Αποφεύγουμε τις
αδυναμίες των δύο παραπάνω ορισμών με τον αξιωματικό ορισμό
της πιθανότητας (Kolmogorov), ο οποίος είναι προιόν
μακροχρόνιων και διαδοχικών βελτιώσεων προγενέστερών του ορισμών.
Ενσωματώνει και επεκτείνει τις ιδιότητες του κλασσικού και του
στατιστικού ορισμού, και προσφέρεται για τη σε βάθος μαθηματική
μελέτη της Θεωρίας Πιθανοτήτων.
Αν και δεν θα αναλύσουμε εδώ αυτόν τον ορισμό,
αναφέρουμε επιγραμματικά τις ιδιότητες/αξιώματα μέσω των οποίων ορίζεται
η πιθανότητα:
. Αποφεύγουμε τις
αδυναμίες των δύο παραπάνω ορισμών με τον αξιωματικό ορισμό
της πιθανότητας (Kolmogorov), ο οποίος είναι προιόν
μακροχρόνιων και διαδοχικών βελτιώσεων προγενέστερών του ορισμών.
Ενσωματώνει και επεκτείνει τις ιδιότητες του κλασσικού και του
στατιστικού ορισμού, και προσφέρεται για τη σε βάθος μαθηματική
μελέτη της Θεωρίας Πιθανοτήτων.
Αν και δεν θα αναλύσουμε εδώ αυτόν τον ορισμό,
αναφέρουμε επιγραμματικά τις ιδιότητες/αξιώματα μέσω των οποίων ορίζεται
η πιθανότητα:
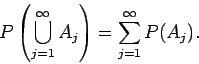
Τα ![]() και
και ![]() είναι ξένα, καθώς και τα
είναι ξένα, καθώς και τα ![]() και
και ![]() . Από το αξίωμα
(iii) του τελευταίου ορισμού της πιθανότητας, έχουμε
. Από το αξίωμα
(iii) του τελευταίου ορισμού της πιθανότητας, έχουμε
![]() , και
, και
![]() .
.
α) Συμβολίζουμε με ![]() ,
, ![]() , και
, και ![]() τα γεγονότα να βγει κόκκινη, άσπρη,
και μπλέ σφαίρα, αντίστοιχα. Ο ΔΧ του πειράματος περιέχει 15 σημεία.
Εάν το καθένα έχει πιθανότητα 1/15, έχουμε ότι
τα γεγονότα να βγει κόκκινη, άσπρη,
και μπλέ σφαίρα, αντίστοιχα. Ο ΔΧ του πειράματος περιέχει 15 σημεία.
Εάν το καθένα έχει πιθανότητα 1/15, έχουμε ότι ![]() ,
επειδή το γεγονός
,
επειδή το γεγονός ![]() περιέχει 6 σημεία του ΔΧ.
περιέχει 6 σημεία του ΔΧ.
β) Με το ίδιο σκεπτικό, ![]() , και
, και
γ) ![]() .
.
δ) Η πιθανότητα να μη βγει κόκκινη σφαίρα είναι ίση με την πιθανότητα
να βγει άσπρη ή μπλε. Έτσι, ![]() όχι
όχι![]() ή
ή
![]() .
Επειδή όμως τα γεγονότα
.
Επειδή όμως τα γεγονότα ![]() και
και ![]() είναι ασυμβίβαστα, θα έχουμε
ότι
είναι ασυμβίβαστα, θα έχουμε
ότι
![]() .
.
ε) Το γεγονός ``![]() ή
ή ![]() '' παριστάνεται από την ένωση των γεγονότων
'' παριστάνεται από την ένωση των γεγονότων
![]() και
και ![]() ,
, ![]() . Αλλά αφού τα
. Αλλά αφού τα ![]() και
και ![]() είναι ασυμβίβαστα, τότε
είναι ασυμβίβαστα, τότε
![]() .
.
Maria Kafesaki 2005-05-26