Research Topics
|
Left-handed materials (LHM) are composite materials whose properties
are not determined by the fundamental physical properties of their constituents
but by the shape and distribution of specific patterns included in them.
LHM have the unique property of having both the effective permittivity
and the effective permeability negative. The aim of the research is
the theoretical understanding, analysis, development, fabrication and
testing of left-handed materials (LHM), and also the investigation of
their feasibility for applications.
Photonic crystals are a class of artificial periodic
composite materials which exhibit electromagnetic band gaps (i.e. frequency
regimes where the EM waves can not propagate). This band gap property
makes the PCs very important for the manipulation of EM waves; they can
act for the EM waves in the same way as the semiconductors for the propagation
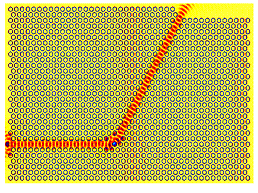
of electrons; e.g., formation of proper defects leads to localized light
modes with desired properties, like guiding of light (by creating linear
defects in PCs – see next figure), storing light in point-like defects etc.
All this ability for light manipulation can be used to improve the functionality
of existing light emitting, receiving and propagating devices, to produce
novel, optimum devices, making even possible the creation of integrated
circuits fully photonic.
Our
tasks in the PC research include study of various PC-based structures
and identification of structures that can be used as components for
the creation of PC integrated circuits; also, exploration of the interaction
of sources with finite PCs, study of defects in PCs, left-handed behaviour
of PCs etc.
Phononic
crystals are the acoustic analogue of photonic crystals. It is going
for periodic composite media with spectral regions where the propagation
of the acoustic and elastic waves is forbidden (phononic band
gaps). Phononic crystals have for the acoustic and elastic waves all
the manipulation capabilities that photonic crystals have for light.
Their most important application is in the creation of acoustic filters,
as the richness in parameters of the acoustic systems gives the ability
for very wide band gaps. Our
current topics on the phononic crystal research include combination
of phononic and photonic band gaps in the same system for the creation
of opto-acoustic devices, characterization of self-assembled colloidal
crystals made of core-shell particles (which can give band gap in sub-wavelength
regimes) and optimization of their properties, negative refraction effects
in phononic crystals etc.
The aim of the present research is the theoretical understanding of the properties of disordered systems,
with emphasis on light localization
and random lasers.
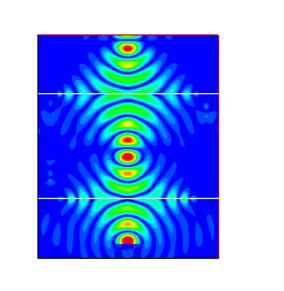
Random Lasers Random
lasers are a combination of strongly scattering media and
an optical gain medium. These systems have many features in common
with conventional lasers based on an optical gain medium enclosed in
a cavity with two mirrors to enhance stimulated emission. In
random lasers, multiple scattering plays the role of the mirrors (see
the figure in the beginning). For example, threshold behavior
for lasing action and frequency narrowing has been observed in random
lasers. Evidently, the optical properties of random lasers are
quite different from conventional lasers; the propagation of pump and
fluorescence light is diffusive, and the absence of a well-defined cavity
with modes along its axis, there is no “preferred direction” in feedback
and loss processes. The ambiguity as to what exactly constitutes
the loss of a random laser, how optical feedback works if it is “omni-directional,”
and the theoretical prediction of an intensity divergence have
led a continuous debate about what happens at, and above, the laser
threshold. We have developed a dynamical approach for understanding
the properties of random lasers, especially above the laser threshold.
We plan to collaborate with experimental groups at Amsterdam and IESL-FORTH
(Laser group) to understand the dynamical behavior of the random laser
systems and check our recent predictions about the shape of the wavefunctions
of random lasers and low threshold lasing in periodic and/or random
materials. It is expected that in the case of a 3d PBG material, the
random feedback effects will be considerably stronger, and can give
lasing with a much lower threshold. We plan to use the inverse opal
structures fabricated at the University of Amsterdam to check these
ideas. We plan to investigate the emission spectra of dopants (such
as Erbium) inside 3d photonic crystals. The situation is reminiscent
of atoms or molecules in 1d Fabry-Perot cavities. The main difference
between Fabry-Perot cavities and photonic crystals is that PC acts as
3d cavities, thereby promising complete control over emission. These
studies will help us develop low threshold lasers and light-emitting
diodes using photonic crystals. One
of the current challenges in laser optics is to take advantage of the
resonant modes within particles to obtain high quality micro-cavities
with low threshold. We have presented a study of the effect that the
internal resonances of individual particles play on the emitted intensity,
and demonstrated how optimal tuning of the size and distances between
the particles can enhance the quality factor by more than 4 orders of
magnitude. The potential applications of this work on the design of
an optimal mirco-cavity and on a random laser are essential. Light
Localization The
analogy between the propagation of electron waves and classical waves
has led to a revival in the research of the transport of light in disordered
scattering systems. The final goal of many of these studies has been
to observe the optical analogue of Anderson localization in electronic
systems. Experimental difficulties in realizing a random medium
where the optical absorption is low enough and the light scattering
is efficient enough to induce localization has been the reason why,
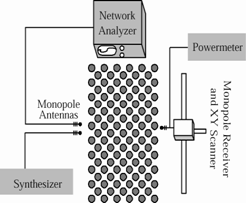
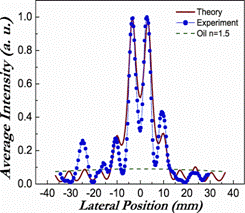
for a long time, only microwave localization was realized. In
light localization experiments, the absorption is large and, therefore,
complicates the interpretation of results. We plan to carry out new
experiments at the University of Amsterdam in very strong scattering
media to clearly distinguish between the effects of optical absorption
and multiple scattering. The effects of finite size and internal
reflection at the boundary of the sample should be also included appropriately.
Currently, experiments are in progress with powders of semiconducting
materials such as Si, Ge and GaP at frequencies near and below the semiconductor
gap of these materials. In addition, a unique porous form of GaP has
recently been developed as well-defined random sample with a connected
network topology. The difference in topology of powders and network
structures and its consequences in localization behavior are still under
study both experimentally and theoretically. To characterize the wave
propagation of light in random media, a variety of optical techniques
have been developed. In particular, the dependence of scattering
properties such as the mean free path as a function of sample thickness,
the enhanced backscattering profiles and speckle correlation techniques
have proven to be essential to augment the static measurements with
time dependent techniques to determine the dynamical transport properties.
For example, short optical pulse transmission measurements are
able to determine the dynamical diffusion constant and properties such
as the effective energy and phase velocity in the medium. We will use
the Energy Density Coherent Potential Approximation developed by K.
Busch, E. N. Economou, Maria Kafesaki and C. M. Soukoulis, to obtain
better estimates for the optimum topology and scatter characteristics.
We also plan to develop the theory of pulse transport in disordered
systems and will be in close contact with the group of Professor Ad
Lagendijk at the University of Amsterdam, which recently moved to University
of Twente.
Nonlinearities Nonlinear
dielectric materials exhibiting a bistable response to intense
radiation are key elements for an all-optical digital technology. We
have used our FDTD methods to study the time-dependent switching properties
of nonlinear systems for constant wave illumination. The conditions
for a fully controlled and reproducible switching were obtained. Our
FDTD methods were also used to study the effects of disorder on the
width of the photonic gaps. It is found that the gaps can survive a
strong amount of disorder. It looks like that short-range order is needed
to have a gap in a photonic crystal.
In
summary, fascinating novel science and technology can be expected from
the synergy of the fields of light localization, photonic band gap materials,
and random lasers. Photonic crystals offer innovative ways to manipulate
light not possible in any previously known photonic material. They represent
the “semiconductors of the future,” and may become the focus
of the photonics revolution of the twenty-first century.
|