|
M.Velegrakis and Ch.Lüder, "Formation and stability of singly and doubly charged MgArN Clusters", Chem. Phys. Lett., 223, 139 (1994)
Ch. Lüder, D. Prekas and M.Velegrakis, “Ion-size effects in the growth sequences of metal-ion-doped noble gas clusters”, Laser Chemistry, 17, 109 (1997)
D. Prekas, Ch. Lüder and M. Velegrakis, ” Structural transitions in metal-ion-doped noble gas clusters: Experiments and molecular dynamics simulations”, J. Chem. Phys. 108, 4450 (1998)
G. E. Froudakis, S. C. Farantos and M. Velegrakis, “ Mass Spectra and Theoretical Modeling of Li+Nen, Li+Arn and Li+Krn Clusters”, Chem. Phys., 258, 13, 2000
M. Velegrakis, “Stability, structure and optical properties of metal ion-doped noble gas clusters”, in : Advances in metal and semiconductor clusters, Chapter 7, Vol. V, ed. M.A. Duncan (JAI Press, Greenwich), June 2001
|
|
Hard Sphere Packing Model |
|
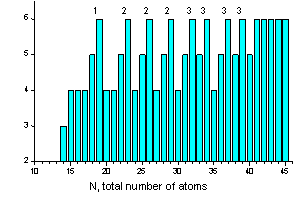
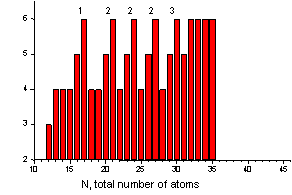
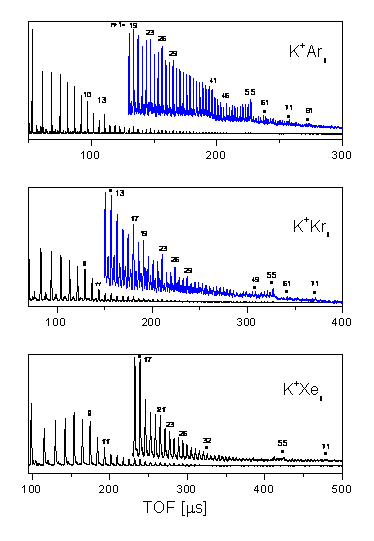
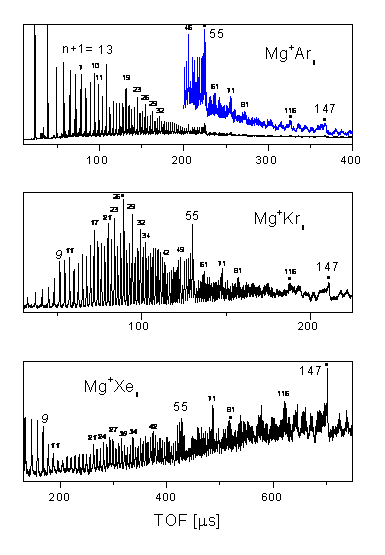
Structural transitions in metal-doped noble gas clusters Using time-of-flight (TOF) mass spectrometry, the stability and the structure of metal ion-doped noble gas clusters M+Xn (M=metal atom and X=noble gas atom) is studied. The observed change in magic number series is explained by a simple hard sphere packing model, showing that the observed new magic numbers are consistent with a cluster growth sequence based on a capped square antiprism (CSA) 11-atomic cluster. Additionally, molecular dynamics simulations using pairwise additive Lennard-Jones potentials are performed. The results of these calculations verify the structural results from the hard sphere model and furthermore explain the structural transition as a function of cluster size.
|
|
Typical TOF spectra of metal ion-doped noble gas clusters of the type M+Xn. The most stable clusters are indicated by the total number of atoms N=n+1. |

|
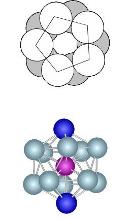
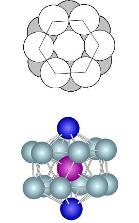
High-symmetry Polyhedra formed from two twisted polygons each of them shaped from n/2 atoms
|
|
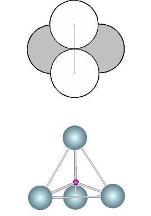
R*=RM/RX=
|
|
0.225
|
|
Tetrahedron n=4
|
|
0.414
|
|
Octahedron antiprism n=8
|
|
n+1 = |
|
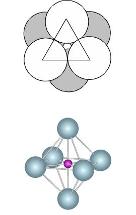
5 |
|
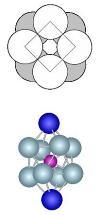
7 |
|
0.645
|
|
Square antiprism n=8 Capped Square antiprism n=8+2 |
|
11 |
|
Pentagonal antiprism n=10 Icosahedron (closed) n=10+2 |
|
0.902
|
|
13 |
|
Hexagonal antiprism n=12 Capped Hexagonal antiprism n=12+2 |
|
1.17 |
|
15 |
|
Schlegel Diagrams explaining cluster growth sequences and magic numbers
|
|
ICOSAHEDRON
|
|
CSA
|