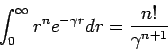Σύγχρονη Φυσική

4. Κβαντομηχανική στις τρεις διαστάσεις

Εδάφια:

4.a. Εξ. Schrodinger στις τρεις διαστάσεις
4.b. Σωμάτιο σε κουτί
4.c. Το άτομο του Υδρογόνου
4.d. Άτομο σε μαγνητικό πεδίο - Spin
4.e. Πολυηλεκτρονικά άτομα - Περιοδικός πίνακας
4.f. Κανόνες επιλογής

4.a. Εξ. Schrodinger στις τρεις διαστάσεις

Άν και η μελέτη της εξ. του Schrodinger στη μία διάσταση αρκεί για να κατανοήσουμε μερικά βασικά χαρακτηριστικά των κβαντομηχανικών συστημάτων, όπως π.χ. η κβάντωση της ενέργειας, δεν επαρκεί αν θέλουμε να μελετήσουμε πιο σύνθετα συστήματα, όπως π.χ. μόρια ή στερεά σώματα. Για μια ρεαλιστική αντιμετώπιση τέτοιων προβλημάτων χρειάζεται να πάμε στον τριδιάστατο "κόσμο", δηλ. να λύσουμε την εξ. Schrodinger στις τρεις διαστάσεις. Η εξίσωση αυτή έχει τη μορφή (χρονοεξαρτημένη)

. (1) Θεωρωντας λύσεις της μορφής

καταλήγουμε στη χρονοανεξάρτητη εξ. Schrodinger:

. (2)

(Ο τελεστής Laplace σε καρτεσιανές συνετεταγμένες έχει τη μορφή )

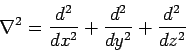Η κυματοσυνάρτηση τώρα είναι μια συνάρτηση του διανύσματος θέσης, ψ(r)=ψ(x,y,z), και το τετράγωνο του πλάτους της εκφράζει την πυκνότητα πιθανότητας (πιθανότητα ανά μονάδα όγκου εδώ) να βρούμε το σωματίδιο σε κάποια περιοχή του χώρου. Το ολοκλήρωμα της σε όλο το χώρο (τριδιάστατο ολοκλήρωμα) είναι μονάδα: .

--------
Τι μονάδες έχει η κυματοσυνάρτηση στις τρεις διαστάσεις;

Επιστροφή στην κορυφή

4.b. Σωμάτιο σε κουτί

Το πιο απλό κβαντομηχανικό πρόβλημα στις τρεις διαστάσεις είναι το πρόβλημα ενός σωματιδίου παγιδευμένου σε κυβικό κουτί ακμής L. Οι επιτρεπτές καταστάσεις ενός τέτοιου σωματιδίου θα δίδονται από τις λύσεις της (2), με V(r)=0 μέσα στο κουτί, και με ψ(x,y,z)=0 για x,y,z > L και x,y,z < 0.

Για τη λύση της εξ. Schrodinger στην πρίπτωση αυτή, και γενικά στα τριδιάστατα προβλήματα, χρησιμοποιούμε τη μέθοδο χωρισμού μεταβλητών. Η βασική αρχή της μεθόδου είναι ότι "όταν η διαφορική εξίσωση μπορεί να γραφεί ως άθροισμα όρων ο καθένας από τους οποίους να είναι συνάρτηση μόνο μίας συντεταγμένης, τότε η λυση μπορεί να γραφεί ως γινόμενο συναρτήσεων της κάθε συντεταγμένης χωριστά". Π.χ. ψ(x,y,x)=ψ_x(x)ψ_y(y)ψ_z(z). Εφαρμόζοντας την αρχή αυτή στο πρόβλημα του σωματιδίου σε κουτί, χρησιμοποιώντας το καρτεσιανό σύστημα (αφού η εξίσωση χωρίζεται στο σύστημα αυτό, και οι συνοριακές συνθήκες εκφράζονται μονοπαραμετρικά, δηλ. συναρτήσει μόνο μίας συντεταγμένης), παίρνουμε τρεις μονοδιάστατες εξισώσεις, κάθε μία από τις οποίες περιγράφει σωμάτιο σε ένα μονοδιάστατο απειρόβαθο πηγάδι εύρους L. Σύμφωνα με τα παραπάνω και λαμβάνοντας υπόψη τις λύσεις του απειρόβαθου πηγαδιού, η κυματοσυνάρτηση του συστήματος (μετά και από κανονικοποίηση) θα είναι

, n, m, l = 1, 2, 3, ... και οι επιτρεπτές ενέργειες του συστήματος

. Οι ακέραιοι n, m, l που εκφράζουν την κβάντωση της ενέργειας λέγονται κβαντικοί αριθμοί.

Ένα νέο φαινόμενο που συναντάμε στα τριδιάστατα προβλήματα, που δεν υπήρχε στη μία διάσταση, είναι το φαινόμενο του εκφυλισμού. Εκφυλισμός σημαίνει ότι σε μία ενεργειακή στάθμη αντιστοιχούν περισσότερες από μία καταστάσεις (δηλαδή περισσότερες από μία κυματοσυναρτήσεις, ή, αλλιώς, περισσότερες από μία διατεταγμένες τριάδες κβαντικών αριθμών. Π.χ. οι καταστάσεις με (n,m,l)=(1,2,1) και (n,m,l)=(2,1,1) έχουν την ίδια ενέργεια). Η πηγή του εκφυλισμού είναι η συμμετρία του συστήματος.

Επιστροφή στην κορυφή

4.c. Το άτομο του Υδρογόνου

Το πιο απλό κβαντομηχανικό ρεαλιστικό σύστημα, το οποίο λύνεται ακριβώς, είναι το άτομο του Υδρογόνου (1 πρωτόνιο και 1 ηλεκτρόνιο). Το δυναμικό στην περίπτωση αυτή οφείλεται στην έλξη πυρήνα-ηλεκτρονίου και είναι δυναμικό Coulomb:

, όπου r είναι η απόσταση ηλεκτρονίου πυρήνα (ο πυρήνας λαμβάνεται ως αρχή των αξόνων). Το κατάλληλο σύστημα συνετεταγμένων για τη μελέτη του προβλήματος αυτού, είναι το σφαιρικό: r=(r,θ,φ) (η εξ. Schrodinger χωρίζεται στο σύστημα αυτό, ενώ δεν χωρίζεται στο καρτεσιανό).

Λύνοντας την εξ. Schrodinger για το άτομο του Υδρογόνου βρίσκουμε τις κυματοσυναρτήσεις που αντιστοιχούν στις επιτρεπτές καταστάσεις του ηλεκτρονίου στο σύστημα,

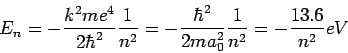, (3) καθώς και τις επιτρεπτές ενέργειες,

με

A. (4)

Όπως φαίνεται από την (3) οι καταστάσεις του συστήματος χαρακτηρίζονται από τρεις κβαντικούς αριθμούς. Ο καθένας από τους αριθμούς αυτούς συνδέεται άμεσα με μία φυσική ποσότητα και εκφράζει την κβάντωση της ποσότητας αυτής. Παρακάτω αναφέρουμε τους κβαντικούς αριθμούς, τα όριά τους και την ποσότητα με την κβάντωση της οποίας συνδέονται.

Κβαντικός αριθμός Όνομα Συνδέεται με Όρια

n κύριος κβαντικός αριθμός Eνέργεια, μέσω της σχέσης 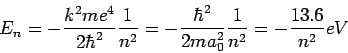1,2,3,...

l τροχιακός ή αζιμουθιακός ή της στροφορμής Μέτρο στροφορμής, μέσω της 0,1,2,...,n-1

m_l μαγνητικός z-συνιστώσα στροφορμής, μέσω της -l,-l+1,...,l-1,l

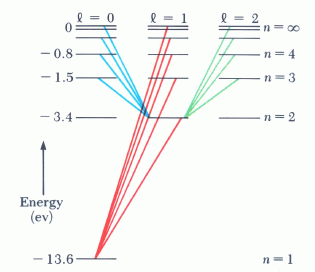
Όπως φαίνεται από την (4) η ενέργεια του σωματιδίου εξαρτάται μόνο από τον κύριο κβαντικό αριθμό, δηλαδή καταστάσεις με το ίδιο n αλλά διαφορετικά l και m_l αντιστοιχούν στην ίδια ενέργεια (εκφυλισμός). Η θεμελιώδης στάθμη αντιστοιχεί σε n=1 και ενέργεια -13.6 eV.

Αν αντί για άτομο Υδρογόνου είχαμε υδρογονοειδές ιόν ατομικού αριθμού Z (Z πρωτόνια και ένα μόνο ηλεκτρόνιο), οι παραπάνω τύποι θα είχαν την ίδια μορφή, με e²-->Ze².

Κεντρικά δυναμικά και κβάντωση στροφορμής: Οι σχέσεις

και

(5) είναι οι συνθήκες κβάντωσης της στροφορμής και ισχύουν για κάθε κεντρικό δυναμικό, V(r)=V(r) (δύναμη στην κατεύθυνση του διανύσματος θέσης). Από τις (5) φαίνεται ότι η γωνία που σχηματίζει το διάνυσμα της στροφορμής με τον άξονα z μπορεί να πάρει μόνο ορισμένες τιμές (είναι κβαντισμένη), τις

. Το φαινόμενο αυτό λέγεται κβάντωση του προσανατολισμού ή της κατεύθυνσης ή του χώρου.

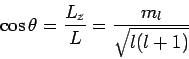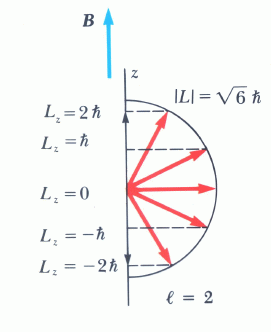
Επιπλέον, η σχέση αβεβαιότητας δεν επιτρέπει το διάνυμα της στροφορμής να είναι απόλυτα καθορισμένο. Μπορούμε να ξέρουμε το μέτρο του και το πολύ μία συνιστώσα του.

Σχ. 1: Η κβάντωση του προσανατολισμού για τροχιακό αριθμό l=2.

------
Ποια είναι η γωνία θ στην κατάσταση μέγιστης ευθυγράμμισης της στροφορμής με τον άξονα z;
--------

Κυματοσυναρτήσεις του Η: Η κυματοσυνάρτηση της θεμελιώδους στάθμης του ατόμου του Η, ψ₁₀₀, είναι σφαιρικά συμμετρική (όπως και όλες οι καταστάσεις με l=0) και έχει τη μορφή (κανονικοποιημένη)

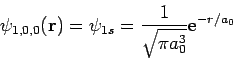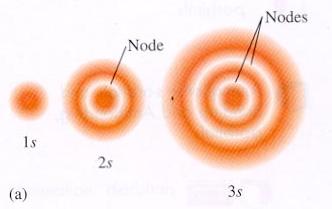. (για υδρογονοειδή άτομα α₀-->α₀/Z). Η μορφή της κυματοσυνάρτησης ψ₁₀₀ στο χώρο δείχνεται στο Σχ. 2 (δείτε την 1s)

.
Σχ. 2: Η μορφή στο χώρο των κυματοσυναρτήσεων ψ₁₀₀ (1s), ψ₂₀₀ (2s) και ψ₃₀₀ (3s).

Εν γένει, αντί να χρησιμοποιούμε στους υπολογισμούς (π.χ. μέσων τιμών θέσης) την πυκνότητα πιθανότητας |ψ(r)|² και να υπολογίζουμε τριδιάστατα ολοκληρώματα, είναι χρήσιμο να εισάγουμε την ακτινική πυκνότητα πιθανότητας, P(r)=4πr²|ψ(r)|² (για σφαιρικά συμμετρικές κυματοσυναρτήσεις), όπου P(r)dr είναι η πιθανότητα να βρεθεί το σωματίδιο στο σφαιρικό φλοιό μεταξύ r και r+dr (). Χρησιμοποιώντας την P(r) μπορούμε να χειριστούμε τα προβλήματα εύρεσης μέσων τιμών ως μονοδιάστατα.

---------
Χρησιμοποιήστε την P(r) για να υπολογίσετε την πιο πιθανή απόσταση του ηλεκτρονίου από τον πυρήνα για τη θεμελιώδη κατάσταση του ατόμου του Η. Υπολογίστε επίσης τη μέση τιμή της απόστασης ηλεκτρονίου-πυρήνα για την ίδια κατάσταση.
---------

Οι καταστάσεις με l>0 είναι καταστάσεις με γωνιακή εξάρτηση. Η γωνιακή αυτή εξάρτηση δεν οφείλεται στην επίδραση του δυναμικού (αφού αυτό είναι σφαιρικά συμμετρικό), και άρα είναι η ίδια για κάθε σφαιρικά συμμετρικό δυναμικό. Συνεπώς για να βρούμε τη γωνιακή εξάρτηση των κυματοσυναρτήσεων μπορooύμε να διαλέξουμε το δυναμικό ώστε η εξ. Schrodinger να οδηγεί στην πολύ πιο απλή εξίσωση grad²=0, την οποία να λύσουμε σε καρτεσιανές συντεταγμένες. Οι λύσεις με την πιο απλή γωνιακή εξάρτηση (εκτός τις σφαιρικά συμμετρικές) είναι οι συναρτήσεις x=r sinθ cosφ, y=rsinθ sinφ, z=rcosθ. Αυτή η γωνιακή εξάρτηση αντιστοιχεί στις καταστάσεις με l=1. Η μορφή τους στο χώρο δείχνεται στο Σχ. 3.

.
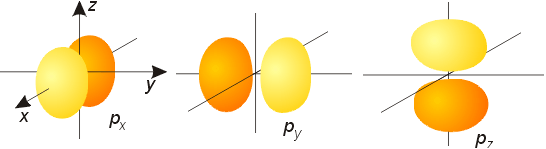Σχ. 3: Η μορφή στο χώρο των κυματοσυναρτήσεων με l=1. Οι p_x και p_y είναι γραμμικοί συνδυασμοί των καταστάσεων με m=1 και -1, και η p_z αντιστοιχεί σε m=0. Για τη μορφή στο χώρο των πιο σύνθετων, όσον αφορά τη γωνιακή εξάρτηση, κυματοσυναρτήσεων δείτε τη σελίδα Grand orbital table.

Φασματοσκοπικός συμβολισμός κυματοσυναρτήσεων: Για το συμβολισμό των κυματοσυναρτήσεων οι φασματοσκόποι χρησιμοποιούν τον κύριο κβαντικό αριθμό (n) και ένα γράμμα, που αντιστοιχεί σε κάθε τιμή του τροχιακού κβαντικού αριθμού l. Η αντιστοιχία δείχνεται στον παρακάτω πίνακα. Επίσης δείχνεται και η γωνιακή εξάρτηση της σχετικής κυματοσυνάρτησης (η γωνιακή εξάρτηση της κυματοσυνάρτησηςη καθορίζεται από την τιμή του l). Οι καταστάσεις σταθερού n, l, m_l χαρακτηρίζονται ως ατομικά τροχιακά.

l Μορφή

l=0 --> s (sharp)
l=1 --> p (principal)
l=2 --> d (diffuse)
l=3 --> f (fundamental)

Παραδείγματα συμβολισμού: ψ_1,0,0 --> 1s, ψ_3,2,1 --> 3d.

και εκπέμποντας φωτόνια. Οι μεταβάσεις αυτές όμως δεν είναι αυθαίρετες αλλα υπακούουν σε κάποιους κανόνες επιλογής. Για να είναι επιτρεπτή μια μετάβαση θα πρέπει οι καταστάσεις μεταξύ των οποίων γίνεται να έχουν

$\begin{displaymath}\Delta l=\pm 1, \hspace{1cm} \Delta m_l=0, \pm\end{disp laymath}$ Αυτό οφείλεται στην αρχή διατήρησης της στροφορμής (σημειώστε ότι το φωτόνιο φέρει μία μονάδα στροφορμής).-->

Επιστροφή στην κορυφή

4.d. Άτομο σε μαγνητικό πεδίο - Spin

Όπως είδαμε πιο πάνω, οι ενεργειακές καταστάσεις του ατόμου του Η και των υδρογονειδών εξαρτώνται μόνο από τον κύριο κβαντικό αριθμό n. Καταστάσεις με το ίδιο n και διαφορετικά l και m αντιστοιχούν στην ίδια ενέργεια (εκφυλισμός). Το φαινόμενο αυτό του εκφυλισμού αίρεται μερικώς όταν το άτομο βρεθεί μέσα σε μαγνητικό πεδίο, Β. Γιατί; Το γεγονός ότι το ηλεκτρόνιο κινείται "γύρω" από τον πυρήνα έχει ως αποτέλεσμα την ύπαρξη στροφορμής και άρα μαγνητικής ροπής, $\begin{displaymath}{\bf\mu}=\displaystyle{-\frac{e}{2m}}{\bf L} \end{displ aymath}$ , (6) δηλαδή το ηλεκτρόνιο συμπεριφέρεται σαν μαγνητάκι, αλληλεπιδρώντας με εξωτερικό μαγνητικό πεδίο. Η δυναμική ενέργεια της αλληλεπίδρασης αυτής, για μαγνητικό πεδίο προσανατολισμένο κατά τον z-αξονα, είναι $\begin{displaymath}U=-{\bf\mu}{\bf B}=-\mu_z B=\displaystyle{-\frac{e\hbar }{2m}}B m_l \end{displaymath}$ (7) Η ενέργεια αυτή προστίθεται στην ενέργεια των "αδιατάρρακτων" καταστάσεων του ηλεκτρονίου στο άτομο. Άρα καταστάσεις με διαφορετικό m_l αποκτούν διαφορετική ενέργεια. Το φαινόμενο αυτό της άρσης του εκφυλισμού μέσα σε μαγνητικό πεδίο λέγεται φαινόμενο Zeeman.

Από την (6) συνεπάγεται $\begin{displaymath}\mu=\displaystyle{-\frac{e}{2m}}\sqrt{l(l+1)}\end{displ aymath}$ (άρα $\begin{displaymath}\mu_z=\displaystyle{-\frac{e\hbar}{2m}}m_l\end{displaym ath}$ , το οποίο χρησιμοποιήθηκε στην (7)), δηλαδή η μαγνητική ροπή είναι πολλαπλάσιο της ποσότητας $\begin{displaymath}\mu_B=\displaystyle{-\frac{e\hbar}{2m}} \end{displaymat h}$ , που λέγεται μαγνητόνη του Bohr και έχει τιμή 9,27x10^-24J/T.

Σημειώστε ότι η κβάντωση και η αρχή της αβεβαιότητας της στροφορμής μεταφέρονται και στη μαγνητική ροπή. Η μαγνητική ροπή δεν μπορεί να είναι απόλυτα ευθυγραμμισμένη με το εξωτερικό μαγνητικό πεδίο, ούτε μπορεί να είναι πλήρως καθορισμένη ως διάνυσμα. Αποδεικνύεται ότι το μ για μια ορισμένη τιμή του κβαντικού αριθμού l εκτελεί μεταπτωτική κίνηση γύρω από τον άξονα του μαγνητικού πεδίου.

Spin: Εκτός από τη στροφορμή λόγω της περιφοράς του γύρω από τον πυρήνα (τροχιακή στροφορμή), το ηλεκτρόνιο, όπως και κάθε άλλο κβαντομηχανικό σωματίδιο, φέρει και μία "εσωτερική" στροφορμή (ιδιοστροφορμή). Η στροφορμή αυτή λέγεται spin και ο πιο ευκολος τρόπος για να την κατανοήσει κανείς είναι να την αποδώσει σε ιδιοπεριστροφή του ηλεκτρονίου (παρόλο που αυτό δεν είναι ακριβώς σωστό).

Στο spin, όπως και στην τροχιακή στροφορμή, αντιστοιχούν επίσης δύο κβαντικοί αριθμοί, s και m_s. O s λέγεται κβαντικός αριθμός του spin, για το ηλεκτρόνιο έχει πάντα την τιμή 1/2, και σχετίζεται με το μέτρο του σπιν σύμφωνα με τη σχέση $\begin{displaymath}S=\vert{\bf S}\vert=\sqrt{s(s+1)}\hbar=(\sqrt{3}/2)\hba r\end{displaymath}$ Ο m_s (ανάλογα με τον m_l) σχετίζεται με την προβολή του σπιν κατά τον άξονα z: $\begin{displaymath}S_z=m_s\hbar\end{displaymath}$ . Ο m_s παίρνει τιμές στο διάστημα [-s,s] (με βήμα 1), άρα για το ηλεκτρόνιο οι δυνατές τιμές του είναι -1/2 και 1/2. Σημειώστε ότι ισχύει κι εδώ η ίδια αρχή αβεβαιότητας και κβάντωση του προσανατολισμού που ισχύει και για την τροχιακή στροφορμή (βλ. Σχ. 3).

Συνέπεια της στροφορμής σπιν είναι η ύπαξη μιας επιπλέον μαγνητικής ροπής για το ηλεκτρόνιο, μ_s (μαγνητική ροπή σπιν), που δίδεται από

$\begin{displaymath}{\bf\mu}_s=\displaystyle{-\frac{e}{m}}{\bf S} =\displaystyle{-\frac{e\hbar}{m}}\sqrt{s(s+1)} \end{displaymath}$ .

Η ύπαρξη του σπιν πρωτοδιαπιστώθηκε το 1921, στο πείραμα των Stern-Gerlach, στο οποίο δέσμη ατόμων Ag σε ανομοιογενές μαγνητικό πεδίο χωρίστηκε σε συνιστώσες διαφορετικές από αυτές που προέβλεπε η κλασική φυσική και η γνωστή τότε κβαντομηχανική, και αποδείχθηκε οριστικά το 1972, με την επανάληψη του ίδιου πειράματος από τους Phipps και Taylor, με χρήση ατόμων υδρογόνου. (Η δύναμη στη δέσμη των ατόμων Η θα δίδεται από (δείτε την (7)) $\begin{displaymath}{\bf F}=-\nabla U=\nabla ({\bf\mu_s}{\bf B})= \mu_{sz}( \partial B_z/\partial z)\hat{z}\end{displaymath}$ (m_l=0).)

Απαγορευτική αρχή του Pauli:. Το ηλεκτρόνιο, όπως και το πρωτόνιο και όλα τα σωματίδια που ανήκουν στα δομικά συστατικά της ύλης, έχει σπιν ημιακέραιο. Τα σωματίδια με σπιν ημιακέραιο ονομάζονται με μια λέξη φερμιόνια. Για τα σωματίδια αυτά ισχύει μια πολύ βασική για τη δομή του κόσμου μας αρχή, η απαγορευτική αρχή του Pauli, η οποία λέει ότι στο ίδιο άτομο δεν είναι δυνατόν να υπάρξουν δύο όμοια φερμιόνια στην ίδια ακριβώς κατάσταση, δηλαδή με όλους τους κβαντικούς αριθμούς ίδιους. Η αρχή αυτή δεν ισχύει για τα σωματίδια με σπιν ακέραιο, τα οποία είναι γνωστά ως μποζόνια. Μποζόνια είναι όλα τα σωματίδια που είναι φορείς δυνάμεων, όπως π.χ. το φωτόνιο, ο φορέας της ηλεκτρομαγνητικής δύναμης, που έχει σπιν 1.

Επιστροφή στην κορυφή

4.e. Πολυηλεκτρονικά άτομα - Περιοδικός πίνακας

Η πιο πάνω απαγορευτική αρχή του Pauli αποτελεί τη βάση για την κατανόηση της ατομικής δομής και των χημικών και φυσικών ιδιοτήτων των στοιχείων. Λόγω της αρχής αυτής σε κάθε ηλεκτρονική κατάσταση ατόμου καθορισμένων n, l, m_l μπορούν να υπάρξουν μόνο δύο ηλεκτρόνια, ένα με m_s=1/2 και ένα με m_s=-1/2. Έτσι, η στάθμη 1s χωράει δύο ηλεκτρόνια, η 2s 2 e, η 2p 6 e (δύο σε κάθε υποστάθμη καθορισμένου n, l, m_l) κοκ.

Όπως είπαμε πιο πάνω, στο άτομο του Υδρογόνου και στα υδρογονοειδή η ενέργεια κάθε κατάστασης εξαρτάται μόνο από τον κύριο κβαντικό αριθμό, n. Τί γίνεται τώρα αν σε ένα άτομο υπάρχουν περισσότερα από ένα ηλεκτρόνια; Τότε εκτός από την έλξη μεταξύ ηλεκτρονίων-πυρήνα υπεισέρχονται στο πρόβλημα και οι ηλεκτροστατικές απώσεις των ηλεκτρονίων. Ένας τρόπος να αντιμετωπίσουμε το πρόβλημα είναι να σκεφτούμε ότι τα ηλεκτρόνια δεν βρίσκονται όλα στην ίδια "απόσταση" από τον πυρήνα. Τα ηλεκτρόνια μικρότερου n βρίσκονται κατά μέσο όρο κοντύτερα στον πυρήνα από ό,τι αυτά με μεγαλύτερο n. Έτσι, στα πιο εξωτερικά ηλεκτρόνια ο πυρήνας δεν θα εμφανίζεται γυμνός αλλά καλυμμένος (θωρακισμένος) από το νέφος των εσωτερικών ηλεκτρονίων. Άρα μια καλή προσέγγιση στο πρόβλημα είναι να θεωρήσουμε ότι τα εξωτερικά ηλεκτρόνια του ατόμου έλκονται από έναν πυρήνα που φέρει "ενεργό φορτίο" Z_eff, όπου Z_eff είναι το φορτίο του πυρήνα (Ζ) θωρακισμένο από το νέφος των εσωτερικότερων ηλεκτρονίων. Στην περίπτωση αυτή το έργο ιονισμού του ατόμου (που ισούται με το αντίθετο της ενέργειας της τελευταίας κατειλημμένης στάθμης) θα δίνεται από

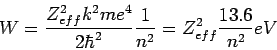$\begin{displaymath}W=\displaystyle{\frac{Z_{eff}^2 k^2 m e^4}{2\hbar^2} \f rac{1}{n^2}}= Z_{eff}^2\frac{13.6}{n^2} eV\end{displaymath}$ , όπου το n είναι ο κύριος κβαντικός αριθμός της τελευταίας κατειλημμένης στάθμης.

Το πιο δραματικό αποτέλεσμα της θωράκισης του πυρήνα από τα ηλεκτρόνια είναι το ότι οι ενέργειες των σταθμών των πολυηλεκτρονικών ατόμων δεν εξαρτώνται πλέον μόνο από τον κύριο κβαντικό αριθμό αλλά και από τον τροχιακό, l. Οι στάθμες με l=1 έχουν υψηλότερη ενέργεια από αυτές με l=0, οι l=2 ακόμα υψηλότερη κ.ο.κ. Το φαινόμενο αυτό δείχνεται στο Σχ. 4.

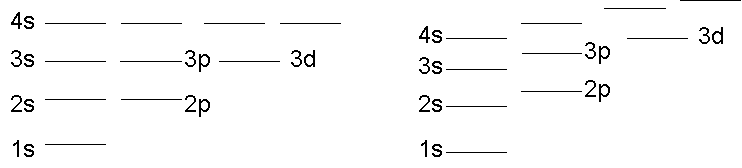
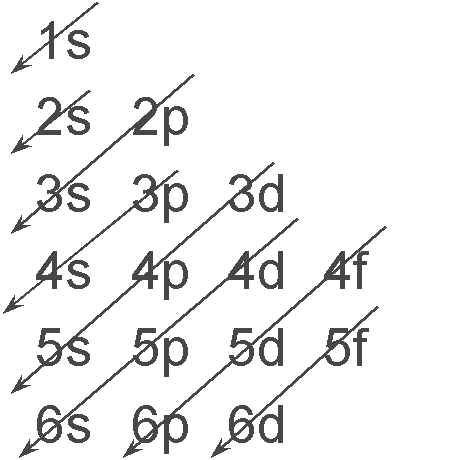
Σχ. 4: Οι ενεργειακές στάθμες υδρογονοειδούς (αριστερά) και πολυηλεκτρονικού ατόμου (δεξιά).

Η ανύψωση των σταθμών αυξανόμενου l στα πολυηλεκτρονικά άτομα έχει ως αποτέλεσμα στάθμες μεγαλύτερου n να βρίσκονται πολλές φορές χαμηλότερα ενεργειακά από στάθμες μικρότερου n με μεγαλύτερο μέτρο στροφορμής. Ένας εύκολος μνημονικός κανόνας για να θυμάται κάποιος την ιεραρχία στην ενέργεια των σταθμών και άρα τον τρόπο συμπλήρωσής τους δείχνεται στο Σχ. 5. Επίσης δείχνεται και ο τρόπος συμπλήρωσης των σταθμών για το άτομο του Ο (Ζ=8).

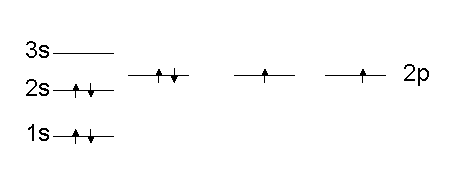
Σχ. 5: Αριστερά: Η σειρά με την οποία συμπληρώνονται οι στάθμες των πολυηλεκτρονικών ατόμων (ακολουθήστε τα βέλη). Δεξιά: Ο τρόπος συμπλήρωσης των σταθμών του ατόμου του Οξυγόνου. Τα βελάκια δείχνουν ηλεκτρόνια με σπιν πάνω και κάτω.

Η συμπλήρωση των υποστοιβάδων της ίδιας ενέργειας (καθορισμένου n και l) γίνεται ακολουθώντας τον κανόνα του Hund, σύμφωνα με τον οποίο οι υποστοιβάδες της ίδιας ενέργειας συμπληρώνονται έτσι ώστε να μεγιστοποιείται ο αριθμός των καταστάσεων που έχουν το ίδιο σπιν. Ένα παράδειγμα δείχνεται το δεξιό από τα Σχήματα 5.

Έχοντας τοποθετήσει τα ηλεκτρόνια του ατόμου στις κατάλληλες στάθμες, μπορεί κανείς να γράψει την ηλεκτρονική διάταξη του ατόμου, χρησιμοποιώντας τον φασματοσκοπικό συμβολισμό, ως [φασματοσκοπικός συμβολισμός στάθμης]^{[αριθμός ηλεκτρονίων]}. Π.χ. η ηλεκτρονική διάταξη του Οξυγόνου (Σχ. 4) γράφεται 1s²2s²2p⁴.

Η χημική συμπεριφορά και η σταθερότητα των ατόμων εξαρτώνται κυρίως από τα ηλεκτρόνια της τελευταίας κατειλημμένης στάθμης τους και από το πόσο εύκολα μπορούν αυτά να μεταπηδήσουν σε άλλη στάθμη ή σε άλλο άτομο και να φτιάξουν χημικό δεσμό (είναι τα λιγότερο δέσμια ηλεκτρόνια). Οι σημαντικοτερες παράμετροι οι οποίοι ρυθμίζουν τη συμπεριφορά των ηλεκτρονίων αυτών και άρα τη χημική συμπεριφορά του ατόμου είναι
1) Ο βαθμός κατάληψης της τελευταίας κατειλημμένης στάθμης.
2) H απόστασή της από την αμέσως απόμενη μη κατειλημμένη στάθμη.
Τα πιο σταθερά άτομα είναι αυτά που η τελευταία στάθμη τους είναι πλήρως κατειλημμένη, με μεγάλη απόσταση από την επόμενη, κενή στάθμη.

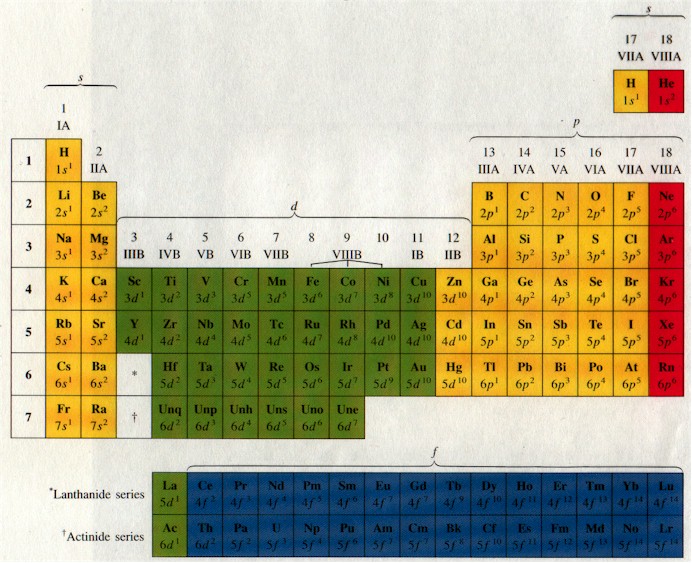
Το περιοδικό σύστημα των στοιχείων (βλ. Σχ. 6) είναι μια κατάταξη των στοιχείων ανάλογα με τις χημικές τους ιδιότητες. Τα στοιχεία που βρίσκονται στην ίδια γραμμή έχουν συμπληρωμένο τον ίδιο φλοιό (ή υποφλοιό) ενώ τα στοιχεία που βρίσκονται στην ίδια στήλη έχουν τον ίδιο βαθμό κατάληψης της τελευταίας στάθμης και άρα παραπλήσιες χημικές ιδιότητες.

Σχ. 6: Ο περιοδικός πίνακας των στοιχείων.

Επιστροφή στην κορυφή

4.f. Κανόνες επιλογής

Στις συνηθισμένες θερμοκρασίες τα ηλεκτρόνια των ατόμων βρίσκονται εν γένει στη θεμελιώδη κατάστασή τους. Αν με κάποιους τρόπους (π.χ. κρούσεις) βρεθούν σε υψηλότερες ενεργειακές (διεγερμένες) καταστάσεις, τείνουν αποδιεγερθούν μεταπίπτοντας σε χαμηλότερες καταστάσεις και εκπέμποντας φωτόνια (τα οποία φέρουν το περίσευμα της ενέργειας). Οι μεταβάσεις αυτές όμως δεν μπορούν να γίνουν αυθαίρετα, αλλα υπακούουν σε κάποιους κανόνες επιλογής. Για να είναι επιτρεπτή μια μετάβαση θα πρέπει οι καταστάσεις μεταξύ των οποίων γίνεται να έχουν

$\begin{displaymath}\Delta l=\pm 1, \hspace{1cm} \Delta m_l=0, \pm\end{disp laymath}$ . Αυτό οφείλεται στην αρχή διατήρησης της στροφορμής σε συνδυασμό με το ότι το φωτόνιο έχει spin 1, δηλαδή φέρει μία μονάδα στροφορμής.

Σχ. 7: Οι διαγώνιες γραμμές δείχνουν μερικές από τις επιτρεπτές μεταβάσεις του ηλεκτρονίου του ατόμου του Υδρογόνου.

Επιστροφή στην κορυφή

Χρήσιμο ολοκλήρωμα σε προβλήματα σχετικά με το άτομο του Υδρογόνου:

$\begin{displaymath}\int_0^{\infty}r^n e^{-\gamma r} dr=\displaystyle{\frac {n!}{\gamma^{n+1}}} \end{displaymath}$

Κβαντικός αριθμός	Όνομα	Συνδέεται με	Όρια
n	κύριος κβαντικός αριθμός	Eνέργεια, μέσω της σχέσης	1,2,3,...
l	τροχιακός ή αζιμουθιακός ή της στροφορμής	Μέτρο στροφορμής, μέσω της	0,1,2,...,n-1
m_l	μαγνητικός	z-συνιστώσα στροφορμής, μέσω της	-l,-l+1,...,l-1,l

l	Μορφή
l=0 --> s (sharp) l=1 --> p (principal) l=2 --> d (diffuse) l=3 --> f (fundamental)