Σύγχρονη Φυσική

3. Κβαντομηχανική στη μία διάσταση

Εδάφια:

3.a. Κυματοσυνάρτηση και κυματική εξίσωση
3.b. Το απειρόβαθο πηγάδι
3.c. Ο αρμονικός ταλαντωτής
3.d. Ορθογώνιο φράγμα δυναμικού

3.a. Κυματοσυνάρτηση και κυματική εξίσωση

Είδαμε στα προηγούμενα ότι η έκφραση "τα σωματίδια έχουν και κυματικό χαρακτήρα" μπορεί να ερμηνευθεί μόνο πιθανοκρατικά, δηλαδή

αυτό που είναι κύμα (απλωμένο) δεν είναι το ίδιο το σωμάτιο αλλά η πιθανότητα να το βρούμε στη μια ή την άλλη περιοχή του χώρου.

Ειδαμε επίσης ότι η κίνηση των κβαντομηχανικών σωματιδίων περιγράφεται από μια κυματοσυνάρτηση, Ψ(x,t), η οποία μετράει την πιθανότητα να βρούμε το σωμάτιο στη μία ή την άλλη περιοχή του χώρου. (Για την ακρίβεια, η πιθανότητα ανά μονάδα μήκους (πυκνότητα πιθανότητας) δίδεται από το τετράγωνο του πλάτους της κυματοσυνάρτησης, |Ψ(x,t)|².)

Η κυματοσυνάρτηση αυτή προκύπτει ως λύση της χαρακτηριστικής εξίσωσης κίνησης των κβαντομηχανικών σωματιδίων, η οποία είναι η εξίσωση Schrodinger. Για ένα σωμάτιο που κινείται σε δυναμικό V(x), η χρονοεξαρτημένη εξίσωση Schrodinger έχει τη μορφή

. (1)

και οι λύσεις της μπορούν να γραφούν ως

(2)

Το χωρικό κομμάτι της κυματοσυνάρτησης, ψ(x), θα ικανοποιεί τη χρονοανεξάρτητη εξίσωση Schrodinger (που προκύπτει αν αντικαταστήσουμε στην χρονοεξαρτημένη εξίσωση την πιο πάνω λύση), η οποία έχει τη μορφή:

(3)

Επειδή από πρόβλημα σε πρόβλημα αυτό που αλλαζει είναι το δυναμικό, το οποίο (αν δεν είναι συνάρτηση του χρόνου) έχει επίδραση μόνο στο χωρικό κομμάτι της κυματοσυνάρτησης και αφήνει ανεπηρέαστο το χρονικό, θα ασχοληθούμε στο εξής κυρίως με το χωρικό κομμάτι της κυματοσυνάρτησης και άρα με λύση της χρονοανεξάρτητης εξίσωσης Schrodinger. (Η χρονική εξέλιξη των κυματοσυναρτήσεων θα σχολιαστεί σε επόμενο βήμα.)

Λίγα επιπλέον σχόλια:

Η κυματοσυνάρτηση στην κβαντομηχανική δεν είναι μετρήσιμο μέγεθος (όπως στα συνήθη κύματα). Αυτό που είναι μετρήσιμο είναι η πυκνότητα πιθανότητας: P(x)=|ψ(x)|².
Η κυματοσυνάρτηση των κβαντομηχανικών σωματιδίων είναι στην χρονοεξαρτημένη μορφή της μιγαδική, ενώ το πραγματικό και το φανταστικό μέρος της χωριστά δεν είναι λύσεις της εξ. Schrodinger (αντίθετα με ό,τι συμβαίνει στα συνήθη κύματα, όπου τα μιγαδικά χρησιμοποιούνται μόνο για διευκόλυνση των πράξεων ενώ η μετρήσιμη ποσότητα είναι το πραγματικό μέρος της κυματοσυνάρτησης, και όπου τόσο το πραγματικό όσο και το φανταστικό μέρος είναι λύσεις της κυματικής εξίσωσης).
Γνωρίζοντας την κυματοσυνάρτηση μπορούμε να βρούμε τη μέση τιμή οποιουδήποτε μεγέθους, f, το οποίο είναι συνάρτηση της θέσης, χρησιμοποιώντας τον ορισμό της μέσης τιμής
Από το ότι η κυματοσυνάρτηση παριστάνει πιθανότητα και από το ότι θα πρέπει να ικανοποιεί την εξ. του Schrodinger, προκύπτει ότι θα πρέπει
- να είναι παντού πεπερασμένη,
- να είναι συνεχής,
- να έχει συνεχή πρώτη παράγωγο (αν το δυναμικό είναι πεπερασμένο),
- να είναι μονότιμη.

Επιστροφή στην κορυφή

3.b. Το απειρόβαθο πηγάδι δυναμικού

Με τον όρο "απειρόβαθο πηγάδι εύρους L" εννούμε το σύστημα στο οποίο ένα σωματίδιο είναι αναγκασμένο να περιοριστεί σε περιοχή εύρους L. Στην περιοχή αυτή το δυναμικό είναι μηδέν ενώ έξω από αυτήν είναι άπειρο.

Στην περιοχή έξω από το πηγάδι η κυματοσυνάρτηση θα πρέπει να είναι μηδέν [για να ισχύει η εξ. (3)], άρα θα είναι μηδέν και στα τοιχώματα του πηγαδιού, x=0, x=L (λόγω συνέχειας). Στο εσωτερικό του πηγαδιού θα ικανοποιεί την ελέυθερη εξίσωση του Schrodinger,

$\begin{displaymath}\displaystyle{-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2 } =E\psi(x)}\end{displaymath}$ . (4)

Η λύσεις της εξίσωσης αυτής με συνοριακές συνθήκες $\begin{displaymath}\psi(0)=\psi(L)=0\end{displaymath}$ είναι οι

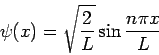$\begin{displaymath}\psi(x)=\displaystyle{\sqrt{\frac{2}{L}}\sin {\frac{n\p i x}{L}}}\end{displaymath}$ , n=1,2,3,..

και οι επιτρεπτές ενέργειες δίνονται από $\begin{displaymath}E_n=\displaystyle{\frac{\hbar^2 \pi^2}{2mL^2}n^2= \frac{h^2}{8mL^2}n^2}\end{displaymath}$

Διάγραμμα των κυματοσυναρτήσεων και των ενεργειακών σταθμών δείχνεται στο Σχ. 1.

Σχ. 1: Κυματοσυναρτήσεις και επιτρεπτές ενέργειες για τις πρώτες στάθμες απειρόβαθου πηγαδιού. Οι κυματοσυναρτήσεις είναι συμμετρικές γύρω από το κέντρο του δυναμικού, πράγμα που ισχύει για κάθε συμμετρικό δυναμικό.

----
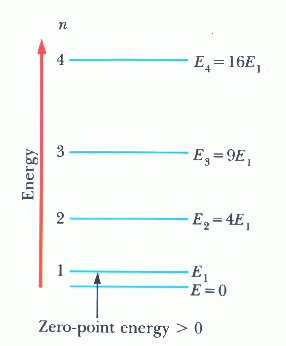
Ποια είναι η διαφορά με την κλασική Φυσική όσον αφορά την ενέργεια της θεμελιώδους κατάστασης απειρόβαθου πηγαδιού;
Πώς βγάζουμε από τη θεωρία του απειρόβαθου πηγαδιού την τάξη μεγέθους των ατομικών και των πυρηνικών ενεργειών;
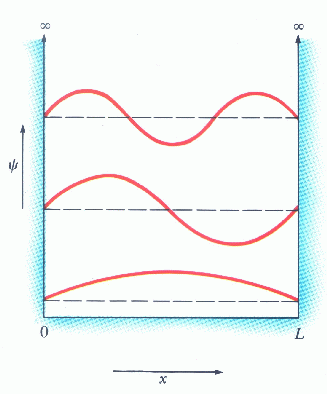
Πόσους κόμβους (σημεία μηδενισμού) έχει η κυματοσυνάρτηση της n-στης διεγερμένης στάθμης του πηγαδιού;
Τι συμμετρία έχουν οι κυματοσυναρτήσεις του πηγαδιού; Πού οφείλεται;
Είναι λογική η εξάρτηση των ενεργειών απειρόβαθου πηγαδιού από τις διάφορες παραμέτρους του προβλήματος; (δίνει το αναμενόμενο κλασικό όριο; εξηγήστε)
----

Μη απειρόβαθο πηγάδι δυναμικού:

Τι γίνεται όταν το δυναμικό στα άκρα πηγαδιού δεν είναι άπειρο (βλ. Σχ. 2); Πώς συγκρίνονται οι κυματοσυναρτήσεις και οι ενέργειες στην περίπτωση αυτή με εκείνες του απειρόβαθου πηγαδιού (βλ. Σχ. 2); Ποια είναι η κλασικά απαγορευμένη περιοχή για το μη απειρόβαθο (πεπερασμένο) πηγάδι; (αναλύστε σε κάθε περίπτωση)

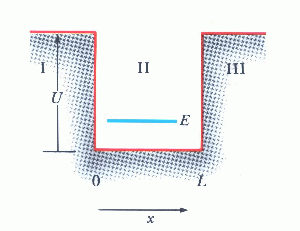
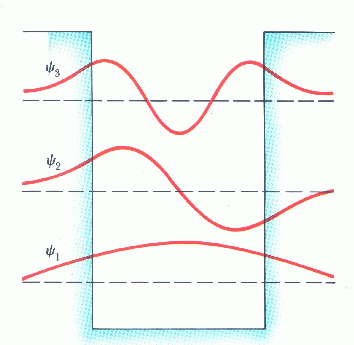
Σχ. 2: Πεπερασμένο πηγάδι δυναμικού (αριστερά) και κυματοσυναρτήσεις για τις πρώτες στάθμες του (δεξιά).

Επιστροφή στην κορυφή

3.c. Ο αρμονικός ταλαντωτής

Είναι το κβαντομηχανικό σύστημα στο οποίο το δυναμικό έχει τη μορφή V(x)=kx²/2=mω²x²/2 (βλ. Σχ. 3). Το δυναμικό αυτό (αρμονικό δυναμικό) προέρχεται από δύναμη της μορφής F(x)=-kx και είναι καλή προσέγγιση κάθε δυναμικού κοντά σε σημεία ευσταθούς ισορροπίας (γιατί;), δηλαδή μπορεί να περιγράψει κάθε είδους μικρές απομακρύνσεις σωμάτων από θέσεις ευσταθούς ισορροπίας.

Σχ. 3: Δυναμικό και ενεργειακές στάθμες αρμονικού ταλαντωτή.

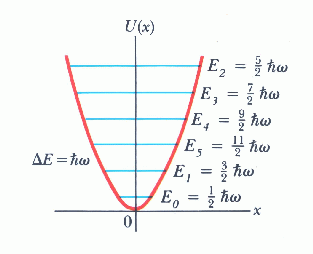
Η εξ. Schrodinger για τον αρμονικό ταλαντωτή (εξ. (3)) είναι μια εξίσωση με μη σταθερούς συντελεστές. Αν και η εύρεση της γενικής λύσης της δεν είναι τόσο απλή, μπορεί κανείς να εξάγει πολλά συμπεράσματα για τις κυματοσυναρτήσεις και τις αντίστοιχες ενέργειες επικαλούμενος μόνο πολύ γενικές ιδιότητες των λύσεων της της εξ. Schrodinger (ποιες;).

Οι κυματοσυναρτήσεις του ταλαντωτή έχουν τη μορφή

, με

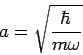
και Η_n(x) πολυώνυμο βαθμού n (n=0,1,2,..). Οι αντίστοιχες ενέργειες δίνονται από

Για τη θεμελιώδη στάθμη, ειδικότερα, έχουμε

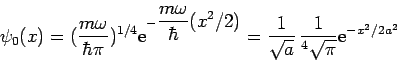και

Μερικά σχόλια:

Ένα από τα βασικά χαρακτηριστικά του αρμονικού δυναμικού είναι οι ισαπέχουσες ενεργειακές στάθμες. Για δυναμικά πιο ευρεία από τον ταλαντωτή οι στάθμες πυκνώνουν καθώς ανεβαίνουμε στο φάσμα (δηλ. καθώς μεγαλώνει το n) ενώ για πιο στενά αραιώνουν.

To αρμονικό δυναμικό, V(x)=kx²/2=Μω²x²/2, περιγράφει πολύ ικανοποιητικά το ταλαντωτικό φάσμα διατομικών μορίων, με x την απόσταση ανάμεσα στους πυρήνες και Μ την ανηγμένη μάζα του μορίου. Η ύπαρξη μη μηδενικής ενέργειας της θεμελιώδους κατάστασης δείχνει ότι τα μόρια, ακόμα και στην κατάσταση ελάχιστης ενέργειας, κάθε άλλο παρά ηρεμούν.

Η τάξη μεγέθους των ταλαντωτικών ενεργειών (δηλ. των ενεργειών των φωτονίων που προέρχονται από μετάβαση από μια ταλαντωτική στάθμη σε άλλη) είναι της τάξης των 1/40 eV (θερμικές ενέργειες, δηλ. υπέρυθρο, αντίθετα με τις ηλεκτρονικές ενέργειες που πέφτουν στο υπεριώδες).

----
Πώς μπορεί κανείς να υπολογίσει την κυματοσυνάρτηση της θεμελιώδους στάθμης ταλαντωτή επικαλούμενος μόνο γενικές ιδιότητες της εξίσωσης Schrodinger και τη συμμετρία του δυναμικού;
Ποια είναι η διαφορά κβαντικού και κλασικού ταλαντωτή όσον αφορά την ενέργεια της θεμελώδους στάθμης;
Ποια είναι η κλασικά απαγορευμένη περιοχή για τον αρμονικό ταλαντωτή;
Πώς ερμηνεύεται η δυνατότητα διείσδυσης των κβαντομηχανικών σωμάτων σε κλασικά απαγορευμένες περιοχές;

Επιστροφή στην κορυφή

3.d. Ορθογώνιο φράγμα δυναμικού

Ορθογώνιο φράγμα δυναμικού είναι μια περιοχή σταθερής δυναμικής ενέργειας, U, που περιβάλλεται από περιοχές χαμηλότερης ή μηδενικής δυναμικής ενέργειας (βλ. Σχ. 4). Αντίθετα από τα προηγούμενα συστήματα, όπου υπήρχε παγίδευση των σωματιδίων και ενδιαφερόμασταν για δέσμιες καταστάσεις, εδώ δεν υπάρχουν δέσμιες καταστάσεις και το πρόβλημα συνίσταται στην εύρεση της πιθανότητας ένα σωματίδιο που προσπίπτει πάνω στο φράγμα να το διαπεράσει ή να ανακλαστεί από αυτό (ή, ισοδύναμα, στην εύρεση του ποσοστού των σωματιδίων που διαπερνούν το φράγμα ή ανακλώνται, θεωρώντας πρόσπτωση πάνω στο φράγμα ρεύματος σωματιδίων).

Στην κλασική φυσική ένα σωματίδιο ενέργειας (Ε) μεγαλύτερης από το ύψος του φράγματος θα το διαπεράσει με πιθανότητα μονάδα, ενώ αν Ε < U θα έχει μηδενική πιθανότητα να το διαπεράσει (το φράγμα είναι κλασικά απαγορευμενη περιοχή). Στην κβαντομηχανική, όπως θα δούμε, σωματίδιο με Ε < U έχει μια μη αμελητέα πιθανότητα να διέλθει μέσω του φράγματος. Το φαινόμενο αυτό της διέλευση σωματιδίων μέσω φραγμάτων δυναμικού λέγεται φαινόμενο σήραγγας και έχει εξαιρετικές εφαρμογές. (Σημειώστε επίσης ότι για Ε > U η κβαντομηχανική πιθανότητα διέλευσης δεν είναι πάντα μονάδα.)

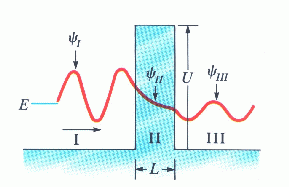
Σχ. 4: Φράγμα δυναμικού και κυματοσυνάρτηση σωματιδίου που προσπίπτει σε αυτό, ερχόμενο από αριστερά.

Για την κβαντομηχανική μελέτη του φράγματος δυναμικού χρειάζεται η επίλυση της εξ. Schrodinger για το σύστημα του Σχ. 4. Λύνοντας την εξ. Schrodinger για τις περιοχές Ι και ΙΙΙ του Σχ. 4 (δηλ. απουσία δυναμικού) και θεωρώντας πρόσπτωση των σωματιδίων (ενέργειας E) από αριστερά του φράγματος, βρίσκουμε για τις αντίστοιχες κυματοσυναρτήσεις τη μορφή

και με

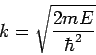
(λαμβάνοντας υπόψη ότι το εκθετικό με το + δηλώνει κύμα που οδεύει προς τα δεξιά και εκείνο με το - κύμα που οδεύει προς τα αριστερά).

Ο λόγος 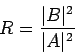$\begin{displaymath}R=\displaystyle{\frac{\vert B\vert^2}{\vert A\vert^2}}\ end{displaymath}$ λέγεται συντελεστής ανάκλασης και δίνει την πιθανότητα ανάκλασης του σωματιδίου (ή αλλιώς το ποσοστό των σωματιδίων που ανακλώνται σε ένα πείραμα σκέδασης)

και ο λόγος 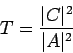$\begin{displaymath}T=\displaystyle{\frac{\vert C\vert^2}{\vert A\vert^2}}\ end{displaymath}$ λέγεται συντελεστής διέλευσης και δίνει την πιθανότητα το σωματίδιο να περάσει το φράγμα και να φθάσει στο x=άπειρο (ή αλλιώς το ποσοστό των σωματιδίων που διέρχονται από το φράγμα). Όπως είναι λογικό R+T=1.

Εν γένει τα R και Τ έχουν σχετικά σύνθετη μορφή και για τον υπολογισμό τους απαιτείται η λύση της εξ. Schrodinger και στην περιοχή ΙΙ (Σχ. 4), και η εφαρμογή κατάλληλων συνοριακών συνθηκών.

Εν τούτοις, για φράγματα αρκετά υψηλά (σε σχέση με την ενέργεια του σωματιδίου) ή αρκετά ευρεία, ο συντελεστής Τ μπορεί να πάρει τη σχετικά απλή μορφή

$\begin{displaymath}T\approx \displaystyle{\mathrm{e}^{-2gL}}\end{displayma th}$ με $\begin{displaymath}g=\sqrt{2m(U-E)/\hbar}\end{displaymath}$ .

Για δυναμικά που εξαρτώνται από τη θέση, U=U(x), στον προηγούμενο τύπο θέτουμε $\begin{displaymath}g L \rightarrow\int_{x_1}^{x_2}\sqrt{2m(U(x)-E)/\hbar}\ end{displaymath}$ .

(Τα x₁, x₂ είναι τα όρια της κλασικά απαγορευμένης περιοχής, E < U .)

Παρατηρήστε ότι ακόμα και για Ε << U ο συντελεστής διέλευσης δεν είναι μηδέν και άρα υπάρχει μία μη μηδενική πιθανότητα το σωματίδιο να περάσει το φράγμα (φαινόμενο σήραγγας).

Παρατηρήστε επίσης την εκθετική ευαισθησία του T στην ενέργεια και τη μάζα του σωματιδίου, καθώς και στο ύψος και το εύρος του φράγματος.

Η ποσότητα δ=1/g λέγεται μήκος διείσδυσης του σωματιδίου και δίνει το εύρος της κλασικά απαγορευμένης περιοχής μέσα στην οποία υπάρχει μετρήσιμη πιθανότητα να βρούμε το σωματίδιο.

Να αναφέρουμε τέλος ότι για Ε > U οι συντελεστές διέλευσης και ανάκλασης είναι επίσης σύνθετες συναρτήσεις της ενέργειας. Είναι αξιοσημείωτο ότι υπάρχει πλήρης διέλευση, Τ=1, μόνο για ορισμένες τιμές ενέργειας του σωματιδίου και ότι οι τιμές αυτές αντιστοιχούν σε αποστάσεις από το ύψος του φράγματος ίσες με τις ιδιοτιμές απειρόβαθου πηγαδιού εύρους L (συντονισμός).

-----
Υπολογίστε το R και το Τ για φράγμα άπειρου εύρους L. (Απάντηση: R=1 και το Τ=0.)
Από ένα ηλεκτρόνιο και ένα πρωτόνιο (ίδιας ενέργειας) που προσπίπτουν στο ίδιο φράγμα δυναμικού ποιο θα έχει μεγαλύτερη πιθανότητα να περάσει το φράγμα;
-----

Εφαρμογές του φαινομένου σήραγγας:

Δίοδοι σήραγγας: Όταν ένα ηλεκτρικό πεδίο εφαρμοστεί σε ένα μέταλλο το μέταλλο αυτό εκπέμπει ηλεκτρόνια. Η εκπομπή αυτή οφείλεται στο ότι με την εφαρμογή του πεδίου το δυναμικό που "βλέπουν" τα ηλεκτρόνια του μετάλλου, από μορφή φράγματος "άπειρου" εύρους, αποκτά τη μορφή πεπερασμένου φράγματος, και άρα γίνεται προσπελάσιμο από τα ηλεκτρόνια.

Δάσπαση άλφα: Είναιη διάσπαση ραδιενεργών στοιχείων με εκπομπή σωματιδίων άλφα (πυρήνων He). Το δυναμικό που φτιάχνει ο συνδυασμος των ισχυρών (ελκτικές και με μικρή εμβέλεια) και των ηλεκτρομαγνητικών δυνάμεων (απωστικές με μεγάλη εμβέλεια) του πυρήνα έχει τη μορφή φράγματος και άρα μπορεί να διαπεραστεί από τα σωματίδια άλφα. (Πως εξηγούνται με βάση τη θεωρία του φράγματος οι μεγάλες διαφορές στους ρυθμούς διάσπασης των ραδιενεργών πυρήνων;)

Σαρωτικό μικροσκόπιο σήραγγας: Είναι διάταξη που επιτρέπει την απεικόνιση επιφανειών με διακριτική ικανότητα της κλίμακας του ατόμου. Φέρει μια πολύ λεπτή (ατομικής κλίμακας) ακίδα από αγώγιμο υλικό. Φέρνοντας την ακίδα του μικροσκοπίου κοντά στην επιφάνεια που θέλουμε να απεικονίσουμε το δυναμικό στην περιοχή μεταξύ ακίδας και επιφάνειας παίρνει τη μορφή φράγματος, επιτρέποντας τη διέλευση ηλεκτρονίων από την επιφάνεια στο μικροσκόπιο (και αντίστροφα, αλλα με εφαρμογή κατάλληλων τάσεων ή υλικών αποτρέπεται η κατεύθυνση αυτή). Η ένταση του ρεύματος που φθάνει στην ακίδα του μικροσκοπίου από την επιφάνεια (άρα που διέρχεται από το φράγμα) εξαρτάται εκθετικά από την απόσταση ακίδας-επιφάνειας. Μετρώντας είτε ρεύμα αυτό είτε την κατακόρυφη κίνηση που θα πρέπει να κάνει η ακίδα για να δέχεται σταθερό ρεύμα, απεικονίζουμε την τοπολογία της επιφάνειας.

Άλλα φαινόμενα που οφείλονται σε διέλευση σήραγγας είναι το ρεύμα σε επαφές Josephson υπεραγωγών, η ταλάντωση του αζώτου στο μόριο της αμμωνίας, η εκπομή ακτινοβολίας από μελανές οπές κ.ο.κ.

Επιστροφή στην κορυφή