Εδάφια:
1.a. Kλασική θεωρία - Ηλεκτρομαγνητικά κύματα
1.b. Ακτινοβολία μέλανος σώματος
1.c. Νόμος του Planck
1.d. Φωτοηλεκτρικό φαινόμενο και φωτόνια
1.e. Φαινόμενο Compton
1.f. Ο κυματοσωματιδιακός δυισμός του φωτός
1.g. Χρήσιμοι μαθηματικοί τύποι
Κλασική θεωρία:
Κάθε σώμα που θερμαίνεται εκπέμπει ακτινοβολία, η οποία σε χαμηλές θερμοκρασίες είναι στο υπέρυθρο (άρα αόρατη) και όσο αυξάνεται η θερμοκρασία μετατοπίζεται προς το ορατό.
Η εκπεμπόμενη θερμική ακτινοβολία εξαρτάται από τη συχνότητα, τη θερμοκρασία και την απορροφούμενη ισχύ (όσο περισσότερο απορροφά ένα σώμα τόσο περισσότερο εκπέμπει).
Το μέλαν σώμα ορίζεται ως ένα αντικείμενο που απορροφά όλη την ακτινοβολία που πέφτει πάνω του, σε όλες τις συχνότητες (για αυτό και φαίνεται μαύρο), Για μέλαν σώμα η εκπεμπόμενη ισχύς είναι συνάρτηση μόνο της συχνότητας (f) και της θερμοκρασίας (T) και είναι μέγιστη. Άρα το μέλαν σώμα είναι ενας ιδανικός εκπομπός, το πρότυπο για να μελετήσει κανείς τη θερμική εκπομπή των σωμάτων (οι τύποι είναι απλούστεροι).
Η καλύτερη αναπαράσταση μέλανος σώματος είναι μια θερμαινόμενη κοιλότητα (π.χ. ένας φούρνος). Αν ανοίξει κανείς μια οπή σε φούρνο, η εκπεμπόμενη ακτινοβολία έχει όλα τα χαρακτηριστικά της ακτινοβολίας μέλανος σώματος.
Σύμφωνα με την κλασική φυσική η ακτινοβολία της κοιλότητας προέρχεται από τις ταλαντώσεις των φορτισμένων σωματιδίων στα τοιχώματα της κοιλότητας και η συχνότητά της είναι ίση με τη συχνότητα των ταλαντώσεων αυτών. Η ενέργεια της ακτινοβολίας μπορεί να πάρει οποιαδήποτε τιμή.
Μεγέθη για την περιγραφή της ακτινοβολίας:
Ι(f,T) είναι η εκπεμπόμενη ισχύς (ενέργεια/χρόνο) ανά μονάδα επιφάνειας και συχνότητας.
u(f,T) είναι η φασματική πυκνότητα ενέργειας, δηλ. η ενέργεια ανά μονάδα συχνότητας και όγκου στην κοιλότητα που αναπαριστά το μέλαν σώμα. I(f,T)=u(f,T) c/4, όπου c η ταχύτητα του φωτός στο κενό.
Τα μεγέθη αυτά μπορούν να γραφούν και ως συνάρτηση του μήκους κύματος, λ, χρησιμοποιώντας τις Ι(λ,T)dλ=Ι(f,T)df, u(λ,T)dλ=u(f,T)df, λ f=c.
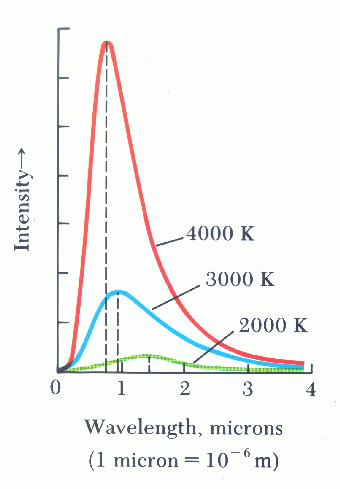
Η ακτινοβολία μέλανος σώματος, I(λ,T), ως συνάρτηση του μήκους κύματος και της θερμοκρασίας έχει τη μορφή που φαίνεται στο Σχ. 1.

Σχ. 1. Ένταση της ακτινοβολίας που εκπέμπεται από μέλαν σώμα ως συνάρτηση της συχνότητας και της θερμοκρασίας.
Βασικά χαρ/κά της ακτινοβολίας μέλανος σώματος - Εμπειρικοί νόμοι
Πρόβλημα: Η ακτινοβολία μέλανος σώματος δεν μπορούσε να περιγραφεί με βάση την υπάρχουσα κλασική θεωρία, κατά την οποία οι υπεύθυνοι για την ακτινοβολία ταλαντωτές (άρα και η ακτινοβολία της κοιλότητας) μπορούν να έχουν οποιαδήποτε ενέργεια, ανεξάρτητα από τη συχνότητά τους.
Το παραπάνω πρόβλημα λύθηκε από τον Planck, ο οποίος έδωσε τον τύπο που περιγράφει σωστά την ακτινοβολία μέλανος σώματος για κάθε περιοχή συχνοτήτων (Για την εργασία του αυτή πήρε το βραβείο Nobel, το 1918.) Οι υποθέσεις-κλειδιά του Planck ήταν:
En=nhf=nhc/λ, n=0,1,2...
που ονομάζονται κβάντα ενέργειας. Οι ταλαντωτές εκπέμπουν ή απορροφούν ενέργεια μόνο όταν "πηδούν" από μια κατάσταση ταλάντωσης σε μια άλλη.u(f,T) = (8 πf2/c3) [hf/(ehf/kT- 1)]
ή μέσω των Ι(λ,T):Ι(λ,T) = (2πc /λ4) [(hc/λ)/(ehc/λkT- 1)].
h είναι η σταθερά του Planck, h=6.67x10-34J.s = 4.11x10-15eV.s. k=kB είναι η σταθερά του Boltzmann, kB=8.6x10-5eV K-1. Σε θερμοκρασία δωματίου, T=300Κ, kBT=(1/40) eV.
H σταθερά κανονικοποίησης, A, στην πιθανότητα P(Ε) προσδιορίζεται από την απαίτηση η ολική πιθανότητα (ολοκλήρωμα σε όλες τις δυνατές ενέργειες) να είναι μονάδα, δηλ. A = 1 / (Integral e-Ε/kBT )
Πιθανότητα και μέση τιμή: Πώς υπολογίζεται η μέση τιμή ενός μεγέθους x (π.χ. Ε) αν γνωρίζουμε την πιθανότητα της κάθε δυνατής τιμής του, P(xn); xav=Σn xn P(xn). Αν το x παίρνει συνεχείς τιμές, P(x) dx είναι η πιθανότητα να είναι μεταξύ x και x+dx και η μέση τιμή είναι xav=Integral x P(x)dx.
Με τον όρο "φωτοηλεκτρικό φαινόμενο" χαρακτηρίζεται η εκπομπή ηλεκτρονίων (φωτοηλεκτρονίων) από ένα μέταλλο όταν πέσει πάνω σε αυτό ορατό ή υπεριώδες φως.
Το "φωτοηλεκτρικό φαινόμενο" ανακαλύφθηκε από τον Hertz (το 1887) και ερμηνεύθηκε α πό τον Αινστάιν (το 1905), ο οποίος πήρε για την ερμηνεία του το Nobel Φυσικής (το 1921).
Πειραματικά δεδομένα για το φωτοηλεκτρικό φαινόμενο (τα οποία δεν μπορούσαν να ερμηνευθούν από την τότε αποδεκτή κλασική θεωρία) είναι τα εξής:
Το φαινόμενο Compton είναι η σκέδαση ηλεκτρομαγνητικής ακτινοβολίας (φωτονίων) από φορτισμένα σωμάτια. Κατά τη σκέδαση αυτή η συχνότητα της σκεδαζόμενης δέσμης (α) είναι μικρότερη από εκείνη της προσπίπτουσας και (β) η μείωση αυτή εξαρτάται από τη γωνία σκέδασης. (Σύμφωνα με την κλασική θεωρία, σκεδαζόμενη και προσπίπτουσα δέσμη θα έπρεπε να έχουν την ίδια συχνότητα.)
Το φαινόμενο Compton ανακαλύφθηκε από τους Debye και Compton, ανεξάρτητα, στις αρχές του 20ου αι. (1923) μελετώντας σκέδαση ακτίνων-X από ελεύθερα ηλεκτρόνια. Η σχηματική αναπαράσταση του φαινόμενου δείχνεται στο παρακάτω σχήμα:
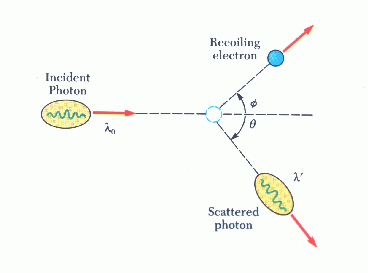
Ο Compton ερμήνευσε το φαινόμενο ως ελαστική κρούση ηλεκτρονίου-φωτονίου (θεωρώντας τα φωτόνια "σημειακά" σωμάτια), και εφαρμόζοντας αρχή διατήρησης ενέργειας και ορμής (σχετικιστικά) κατέληξε στην εξής εξίσωση του φαινομένου Compton:
λc= (h / mec)=0.0243 Α είναι το μήκος κύματος Compton του ηλεκτρονίου.
Η ανακάλυψη και η ερμηνεία του φαινομένου Compton έδωσαν στον Compton, το 1927, το βραβείο Nobel.
Το φως έχει και κυματικό και σωματιδιακό χαρακτήρα (αποτελείται από αδιαίρετα "πακέτα" που φέρουν ενέργεια και ορμή, τα φωτόνια ή κβάντα φωτός).
Οι βασικές σχέσεις που συνδέουν τα κυματικά χαρακτηριστικά του (συχνότητα (f), μήκος κύματος (λ)) με τα σωματιδιακά του χαρακτηριστικά (ενέργεια (E), ορμή (p)) είναι οι εξής:
(Για το φως Ε=pc και άρα λf=c. Η σχέση Ε=pc προκύπτει από τη γενική σχετικιστική σχέση ενέργειας-ορμής, Ε2=p2c2 +m2c4, για σωμάτια χωρίς μάζα, m=0.)
Σχετικιστική κινητική ενέργεια: Κ=sqrt(p2c2
+m2c4)-mc2=γ mc2. Για v<< c ,
Κ=p2/2m
Μαθηματικοί τύποι:
(1+x)n= 1+nx+..., για x<<1
exp(x)= 1+x+x2/2!..., για x<<1
ln(1+x)= x-x2/2!+...
sin(θ)= θ-θ3/3!+...
cos(θ)= 1-θ2/2!+...
tan(θ) =θ+θ3/3+...