Θεωρούμε ένα πείραμα τύχης στο οποίο ρίχνουμε ένα νόμισμα τρείς
φορές, με πιθανότητα 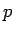 να εμφανιστούν γράμματα (Γ) σε κάθε ρίψη
(σε ένα ``τίμιο'' νόμισμα η πιθανότητα αυτή θα είναι 1/2).
Υποθέστε ότι αν σε μια ρίψη εμφανιστούν Γ κερδίζουμε 1 ευρώ,
ενώ αν εμφανιστεί κεφάλι (Κ) χάνουμε 1 ευρώ.
Προφανώς η ποσότητα που μας ενδιαφέρει εδώ, και την οποία
συμβολίζουμε με
να εμφανιστούν γράμματα (Γ) σε κάθε ρίψη
(σε ένα ``τίμιο'' νόμισμα η πιθανότητα αυτή θα είναι 1/2).
Υποθέστε ότι αν σε μια ρίψη εμφανιστούν Γ κερδίζουμε 1 ευρώ,
ενώ αν εμφανιστεί κεφάλι (Κ) χάνουμε 1 ευρώ.
Προφανώς η ποσότητα που μας ενδιαφέρει εδώ, και την οποία
συμβολίζουμε με  , είναι το συνολικό μας κέρδος.
Είναι φανερό ότι η
, είναι το συνολικό μας κέρδος.
Είναι φανερό ότι η  μπορεί να πάρει μόνο μία από τις τιμές:
3, 1, -3, και -1. Το ποια από αυτές θα πάρει εξαρτάται από το
αποτέλεσμα του τυχαίου πειράματος. Αν, για παράδειγμα, το αποτέλεσμα
είναι ΓΓΓ η
μπορεί να πάρει μόνο μία από τις τιμές:
3, 1, -3, και -1. Το ποια από αυτές θα πάρει εξαρτάται από το
αποτέλεσμα του τυχαίου πειράματος. Αν, για παράδειγμα, το αποτέλεσμα
είναι ΓΓΓ η  παίρνει την τιμή 3, ενώ αν είναι ΓΚΓ
η
παίρνει την τιμή 3, ενώ αν είναι ΓΚΓ
η  παίρνει την τιμή 1.
Στον παρακάτω πίνακα καταγράφουμε τις τιμές της
παίρνει την τιμή 1.
Στον παρακάτω πίνακα καταγράφουμε τις τιμές της  που αντιστοιχούν
στα οκτώ δυνατά αποτελέσματα,
που αντιστοιχούν
στα οκτώ δυνατά αποτελέσματα, 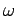 , του τυχαίου πειράματος, καθώς και την
πιθανότητα να εμφανιστεί καθένα από τα αποτελέσματα αυτά
(σημειώστε ότι ο αριθμός των δυνατών αποτελεσμάτων είναι ο αριθμός των δυνατών
τριάδων που μπορούμε να φτιάξουμε από τα δύο στοιχεία,
Γ, Κ, οι οποίες, σύμφωνα με τη θεωρία του προηγούμενου κεφαλαίου,
είναι
, του τυχαίου πειράματος, καθώς και την
πιθανότητα να εμφανιστεί καθένα από τα αποτελέσματα αυτά
(σημειώστε ότι ο αριθμός των δυνατών αποτελεσμάτων είναι ο αριθμός των δυνατών
τριάδων που μπορούμε να φτιάξουμε από τα δύο στοιχεία,
Γ, Κ, οι οποίες, σύμφωνα με τη θεωρία του προηγούμενου κεφαλαίου,
είναι
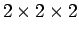 ).
).
(Στον παραπάνω πίνακα, η πιθανότητα του αποτελέσματος ΓΓΓ
υπολογίστηκε ως γινόμενο των πιθανοτήτων των τριών ανεξάρτητων
ενδεχομένων 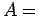 ''στην πρώτη ρίψη Γ'',
''στην πρώτη ρίψη Γ'', 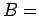 ``στη δεύτερη ρίψη Γ'',
``στη δεύτερη ρίψη Γ'',
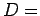 ''στην τρίτη ρίψη Γ'', λαμβάνοντας υπόψη ότι η πιθανότητα της
τομής ανεξάρτητων
ενδεχομένων ισούται με το γινόμενο των πιθανοτήτων τους.
Ανάλογα για τα άλλα αποτελέσματα.)
''στην τρίτη ρίψη Γ'', λαμβάνοντας υπόψη ότι η πιθανότητα της
τομής ανεξάρτητων
ενδεχομένων ισούται με το γινόμενο των πιθανοτήτων τους.
Ανάλογα για τα άλλα αποτελέσματα.)
Μπορούμε να σκεφτόμαστε τη  ως μια πραγματική μεταβλητή η οποία
για κάθε στοιχειώδες
ενδεχόμενο
ως μια πραγματική μεταβλητή η οποία
για κάθε στοιχειώδες
ενδεχόμενο 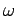 του
του 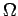 παίρνει μια ορισμένη τιμή (εδώ
μια από τις τιμές
-3,-1,1,3). Η πιθανότητα η
παίρνει μια ορισμένη τιμή (εδώ
μια από τις τιμές
-3,-1,1,3). Η πιθανότητα η  να πάρει μια ορισμένη τιμή, έστω 1,
είναι η πιθανότητα του γεγονότος
να πάρει μια ορισμένη τιμή, έστω 1,
είναι η πιθανότητα του γεγονότος
 το οποίο περιλαμβάνει όλα τα στοιχειώδη
ενδεχόμενα
το οποίο περιλαμβάνει όλα τα στοιχειώδη
ενδεχόμενα 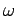 του
του 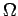 που οδηγούν στην τιμη
που οδηγούν στην τιμη 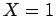 (στο παράδειγμά μας τα ΓΓΚ, ΓΚΓ και ΚΓΓ).
Από τον πίνακα βλέπουμε ότι το
(στο παράδειγμά μας τα ΓΓΚ, ΓΚΓ και ΚΓΓ).
Από τον πίνακα βλέπουμε ότι το 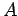 έχει πιθανότητα
έχει πιθανότητα
 να πραγματοποιηθεί (το
να πραγματοποιηθεί (το 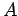 είναι η ένωση των
ανεξάρτητων ενδεχομένων ΓΓΚ, ΓΚΓ και ΚΓΓ).
Ανάλογα μπορούμε να χειριστούμε
και τις υπόλοιπες τιμές της
είναι η ένωση των
ανεξάρτητων ενδεχομένων ΓΓΚ, ΓΚΓ και ΚΓΓ).
Ανάλογα μπορούμε να χειριστούμε
και τις υπόλοιπες τιμές της  . Έτσι, για κάθε τιμή που
μπορεί να πάρει η
. Έτσι, για κάθε τιμή που
μπορεί να πάρει η  , έστω
, έστω 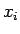 (που εδώ θα είναι κάποιο από τα
(που εδώ θα είναι κάποιο από τα
 ), η πιθανότητα με την οποία παίρνει αυτή
την τιμή,
), η πιθανότητα με την οποία παίρνει αυτή
την τιμή, 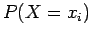 , είναι πλήρως καθορισμένη (π.χ.
, είναι πλήρως καθορισμένη (π.χ.
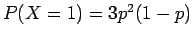 ).
Θα δούμε ότι η
).
Θα δούμε ότι η  είναι ένα παράδειγμα διακριτής τυχαίας
μεταβλητής (ή στοχαστικής συνάρτησης, όπως επίσης λέγεται).
είναι ένα παράδειγμα διακριτής τυχαίας
μεταβλητής (ή στοχαστικής συνάρτησης, όπως επίσης λέγεται).
Ορισμός: Διακριτή τυχαία μεταβλητή  σε ένα
δειγματοχώρο
σε ένα
δειγματοχώρο 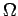 είναι μια μεταβλητή
είναι μια μεταβλητή  που ορίζεται για
κάθε δυνατό αποτέλεσμα ενός τυχαίου πειράματος και για κάθε τέτοιο
αποτέλεσμα παίρνει μια ορισμένη τιμή από ένα πεπερασμένο ή άπειρο
αριθμήσιμο υποσύνολο
των πραγματικών αριθμών.
που ορίζεται για
κάθε δυνατό αποτέλεσμα ενός τυχαίου πειράματος και για κάθε τέτοιο
αποτέλεσμα παίρνει μια ορισμένη τιμή από ένα πεπερασμένο ή άπειρο
αριθμήσιμο υποσύνολο
των πραγματικών αριθμών.
Ορισμός: Η πραγματική συνάρτηση 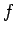 που ορίζεται
στους πραγματικούς αριθμούς από την
που ορίζεται
στους πραγματικούς αριθμούς από την 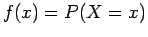 ,
λέγεται διακριτή συνάρτηση πυκνότητας ή συνάρτηση πιθανότητας
ή κατανομή πιθανότητας της
,
λέγεται διακριτή συνάρτηση πυκνότητας ή συνάρτηση πιθανότητας
ή κατανομή πιθανότητας της  (Δίνει την πιθανότητα η
(Δίνει την πιθανότητα η  να πάρει
μια ορισμένη τιμή από το πεδίο τιμών της.
Π.χ., για την τυχαία μεταβλητή
να πάρει
μια ορισμένη τιμή από το πεδίο τιμών της.
Π.χ., για την τυχαία μεταβλητή
 που ορίσαμε στην αρχή του κεφαλαίου
που ορίσαμε στην αρχή του κεφαλαίου 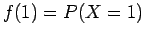 δίνει την
πιθανότητα η
μεταβλητή
δίνει την
πιθανότητα η
μεταβλητή  (το κέρδος) να πάρει την τιμή 1 (να είναι 1 ευρώ).)
(το κέρδος) να πάρει την τιμή 1 (να είναι 1 ευρώ).)
Ας θεωρήσουμε την τυχαία μεταβλητή
 που ορίσαμε στην αρχή του κεφαλαίου, και ας υποθέσουμε ότι
που ορίσαμε στην αρχή του κεφαλαίου, και ας υποθέσουμε ότι  .
Τότε η
.
Τότε η  έχει τη διακριτή συνάρτηση πυκνότητας που ορίζεται
από τις
έχει τη διακριτή συνάρτηση πυκνότητας που ορίζεται
από τις
και 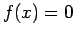 , αν
, αν
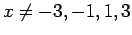 .
H συνάρτηση πυκνότητας ή απλά πυκνότητα
.
H συνάρτηση πυκνότητας ή απλά πυκνότητα 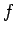 μιας διακριτής
τυχαίας μεταβλητής έχει τις ακόλουθες ιδιότητες:
μιας διακριτής
τυχαίας μεταβλητής έχει τις ακόλουθες ιδιότητες:
- (1)
-
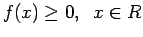
- (2)
- To σύνολο
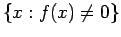 (δηλαδή το σύνολο των τιμών της
(δηλαδή το σύνολο των τιμών της
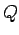 που έχουν μη μηδενική πιθανότητα) είναι ένα πεπερασμένο
ή άπειρο αριθμήσιμο υποσύνολο του
που έχουν μη μηδενική πιθανότητα) είναι ένα πεπερασμένο
ή άπειρο αριθμήσιμο υποσύνολο του  .
Έστω
.
Έστω
 αυτό το σύνολο. Τότε
αυτό το σύνολο. Τότε
- (3)
-
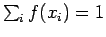 .
.
Οι ιδιότητες (1) και (2) προκύπτουν άμεσα από τον ορισμό της 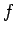 .
Για να δούμε αν ισχύει η (3) παρατηρούμε ότι τα ενδεχόμενα
.
Για να δούμε αν ισχύει η (3) παρατηρούμε ότι τα ενδεχόμενα
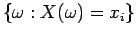 (δηλαδή τα ενδεχομενα του
(δηλαδή τα ενδεχομενα του
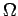 που δίδουν για τη
που δίδουν για τη 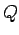 την τιμή
την τιμή 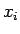 ) είναι ξένα και η
ένωσή τους είναι
το
) είναι ξένα και η
ένωσή τους είναι
το 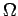 . Άρα
. Άρα
Έτσι, μπορούμε να ορίσουμε εναλλακτικά την πυκνότητα 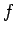 ως εξής:
ως εξής:
Ορισμός:
Μια πραγματική συνάρτηση 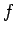 ορισμένη στο
ορισμένη στο  λέγεται διακριτή
συνάρτηση πυκνότητας ή απλά διακριτή πυκνότητα αν ικανοποιεί
τις παραπάνω ιδιότητες (1) - (3).
λέγεται διακριτή
συνάρτηση πυκνότητας ή απλά διακριτή πυκνότητα αν ικανοποιεί
τις παραπάνω ιδιότητες (1) - (3).
-
- Παράδειγμα 1:
Ρίχνουμε ένα νόμισμα δύο φορές, και ορίζουμε την τυχαία μεταβλητή
 ως το πλήθος των Κ που εμφανίστηκαν. Να υπολογιστεί η
πυκνότητα
ως το πλήθος των Κ που εμφανίστηκαν. Να υπολογιστεί η
πυκνότητα 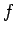 της
της  .
.
Η αντιστοιχία μεταξύ των δυνατών αποτελεσμάτων του πειράματος
και των τιμών της διακριτής τυχαίας μεταβλητής  δίνεται
στον παρακάτω πίνακα, μαζί με την πιθανότητα των σημείων του
δειγματοχώρου
δίνεται
στον παρακάτω πίνακα, μαζί με την πιθανότητα των σημείων του
δειγματοχώρου 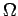 του πειράματος.
του πειράματος.
Η πυκνότητα που αντιστοιχεί στη  είναι
είναι
και 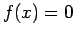 για
για 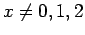 . Προσέξτε ότι
. Προσέξτε ότι
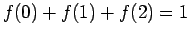 .
Η γραφική παράσταση της
.
Η γραφική παράσταση της 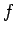 δίνεται είτε με ένα ραβδόγραμμα,
είτε με ένα ιστόγραμμα.
Σε ένα ραβδόγραμμα το άθροισμα των τεταγμένων είναι 1,
ενώ σέ ένα ιστόγραμμα το άθροισμα των εμβαδών είναι 1,
όπως προκύπτεί από την ιδιότητα (3).
Σε ένα ιστόγραμμα μπορούμε να φανταστούμε ότι η τυχαία μεταβλητή
δίνεται είτε με ένα ραβδόγραμμα,
είτε με ένα ιστόγραμμα.
Σε ένα ραβδόγραμμα το άθροισμα των τεταγμένων είναι 1,
ενώ σέ ένα ιστόγραμμα το άθροισμα των εμβαδών είναι 1,
όπως προκύπτεί από την ιδιότητα (3).
Σε ένα ιστόγραμμα μπορούμε να φανταστούμε ότι η τυχαία μεταβλητή
 γίνεται συνεχής, λόγου χάρη
γίνεται συνεχής, λόγου χάρη 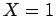 σημαίνει ότι η
σημαίνει ότι η  είναι
μεταξύ 0.5 και 1.5.
είναι
μεταξύ 0.5 και 1.5.
Σημειώστε ότι και άλλες τυχαίες μεταβλητές μπορούν να οριστούν στον
ίδιο δειγματοχώρο 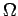 . Λόγου χάρη, στο προηγούμενο παράδειγμα
θα μπορούσαμε να ορίσουμε μια τυχαία μεταβλητή
. Λόγου χάρη, στο προηγούμενο παράδειγμα
θα μπορούσαμε να ορίσουμε μια τυχαία μεταβλητή 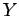 ως το πλήθος
των Κ που εμφανίζονται μείον το πλήθος των Γ που εμφανίζονται.
Τότε, οι δυνατές τιμές της
ως το πλήθος
των Κ που εμφανίζονται μείον το πλήθος των Γ που εμφανίζονται.
Τότε, οι δυνατές τιμές της 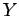 θα ήταν -2,0,2, ενώ η αντίστοιχη
πυκνότητα θα έπαιρνε τις τιμές
θα ήταν -2,0,2, ενώ η αντίστοιχη
πυκνότητα θα έπαιρνε τις τιμές
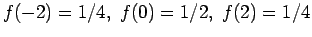 και
και 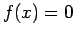 για
για 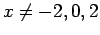 .
.
Κάθε διακριτή συνάρτηση πυκνότητας, δηλαδή κάθε συνάρτηση που
ικανοποιεί τις ιδιότητες (1) - (3), είναι η πυκνότητα κάποιας
τυχαίας μεταβλητής  . Με άλλα λόγια, αν μας δοθεί η
. Με άλλα λόγια, αν μας δοθεί η 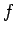 μπορούμε πάντα να κατασκευάσουμε ένα δειγματοχώρο
μπορούμε πάντα να κατασκευάσουμε ένα δειγματοχώρο 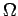 και
μια τυχαία μεταβλητή ορισμένη στον
και
μια τυχαία μεταβλητή ορισμένη στον 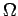 , της οποίας η διακριτή
πυκνότητα να είναι
, της οποίας η διακριτή
πυκνότητα να είναι 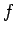 . Έτσι μπορούμε να χρησιμοποιούμε
εκφράσεις όπως ``έστω
. Έτσι μπορούμε να χρησιμοποιούμε
εκφράσεις όπως ``έστω  μια τυχαία μεταβλητή με διακριτή
πυκνότητα
μια τυχαία μεταβλητή με διακριτή
πυκνότητα 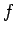 ''
χωρίς να διευκρινίζουμε τον δειγματοχώρο
''
χωρίς να διευκρινίζουμε τον δειγματοχώρο 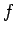 στον οποίο ορίζεται
η
στον οποίο ορίζεται
η  . Για παράδειγμα, υποθέστε ότι επιλέγουμε ένα χαρτί από μια
δεσμίδα με
. Για παράδειγμα, υποθέστε ότι επιλέγουμε ένα χαρτί από μια
δεσμίδα με 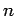 χαρτιά, και θέτουμε
χαρτιά, και θέτουμε 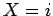 αν επιλεγεί το
αν επιλεγεί το
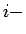 οστο χαρτί. Τότε,
οστο χαρτί. Τότε, 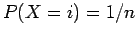 , άρα μπορούμε να περιγράψουμε
το πείραμα λέγοντας ότι παρατηρούμε μια τυχαία μεταβλητή
, άρα μπορούμε να περιγράψουμε
το πείραμα λέγοντας ότι παρατηρούμε μια τυχαία μεταβλητή  η οποία παίρνει ακέραιες τιμές
η οποία παίρνει ακέραιες τιμές 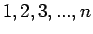 και έχει πυκνότητα
και έχει πυκνότητα
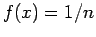 αν
αν 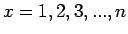 και
και 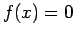 αλλιώς.
αλλιώς.
Γενικά, κάθε τυχαίο πείραμα που έχει πεπερασμένα ή άπειρα αριθμήσιμα
το πλήθος δυνατά αποτελέσματα μπορεί να περιγραφεί ως η παρατήρηση
της τιμής μιας διακριτής τυχαίας μεταβλητής  .
Για την ακρίβεια, το πείραμα πολλές φορές μας δίνεται ήδη μ' αυτή τη
μορφή.
.
Για την ακρίβεια, το πείραμα πολλές φορές μας δίνεται ήδη μ' αυτή τη
μορφή.
Στα δύο επόμενα παραδείγματα παρουσιάζονται δύο τυπικές
διακριτές πυκνότητες.
-
- Παράδειγμα 2: Η γεωμετρική πυκνότητα.
Έστω 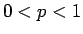 . Τότε η πραγματική συνάρτηση
. Τότε η πραγματική συνάρτηση 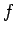 που ορίζεται στο
που ορίζεται στο
 από την
από την
είναι μια διακριτή πυκνότητα και λέγεται γεωμετρική πυκνότητα
με παράμετρο 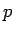 .
.
Για να δούμε αν η 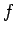 είναι πυκνότητα, το μόνο που χρειάζεται
να ελέγξουμε είναι ότι ισχύει η ιδιότητα (3), αφού οι (1) και (2)
ικανοποιούνται προφανώς. Όμως,
είναι πυκνότητα, το μόνο που χρειάζεται
να ελέγξουμε είναι ότι ισχύει η ιδιότητα (3), αφού οι (1) και (2)
ικανοποιούνται προφανώς. Όμως,
αφού το άθροισμα της γεωμετρικής σειράς
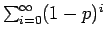 είναι ίσο με
είναι ίσο με 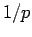 .
.
-
- Παράδειγμα 3: Η πυκνότητα Poisson.
Έστω 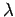 ένας θετικός αριθμός. Η πυκνότητα Poisson
με παράμετρο
ένας θετικός αριθμός. Η πυκνότητα Poisson
με παράμετρο 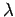 ορίζεται από τη σχέση
ορίζεται από τη σχέση
Η συνάρτηση 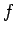 προφανώς ικανοποιεί τις (1) και (2) του ορισμού
της διακριτής συνάρτησης πυκνότητας. Για να δούμε αν ισχύει η (3)
θα χρησιμοποιήσουμε το ανάπτυγμα Taylor της εκθετικής συνάρτησης
προφανώς ικανοποιεί τις (1) και (2) του ορισμού
της διακριτής συνάρτησης πυκνότητας. Για να δούμε αν ισχύει η (3)
θα χρησιμοποιήσουμε το ανάπτυγμα Taylor της εκθετικής συνάρτησης
Έτσι,
Η εμπειρία δείχνει ότι πολλά τυχαία φαινόμενα που έχουν σχέση με το
μέτρημα ακολουθούν κατά προσέγγιση την κατανομή Poisson, όπως
για παράδειγμα τα εξής:
- (α)
- Tο πλήθος των ατόμων μιας ραδιενεργού ουσίας που αποσυντίθενται
στη μονάδα του χρόνου.
- (β)
- Tο πλήθος των κλήσεων που δέχεται ένα τηλεφωνικό κέντρο
στη μονάδα του χρόνου. (Δηλαδή η πιθανότητα το πλήθος των κλήσεων
που δέχεται το τηλεφωνικό κέντρο να είναι
 δίνεται από το
δίνεται από το
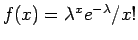 .)
.)
- (γ)
- Το πλήθος των τυπογραφικών λαθών σε μια σελίδα ενός βιβλίου,
κ.τ.λ.
Η αθροιστική συνάρτηση κατανομής ή απλά συνάρτηση κατανομής
για μια τυχαία μεταβλητή  ορίζεται από τη σχέση
ορίζεται από τη σχέση
όπου 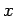 οποιοσδήποτε πραγματικός αριθμός (
οποιοσδήποτε πραγματικός αριθμός (
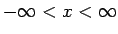 ).
Η συνάρτηση κατανομής μπορεί να υπολογιστεί από την πυκνότητα
).
Η συνάρτηση κατανομής μπορεί να υπολογιστεί από την πυκνότητα 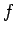 ,
επειδή
,
επειδή
όπου το άθροισμα στο δεξιό μέλος νοείται ως προς όλα τα 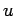 για
τα οποία
για
τα οποία 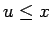 . Αντίστροφα, η πυκνότητα μπορεί να προκύψει από τη
συνάρτηση κατανομής, όπως θα δούμε και στο επόμενο παράδειγμα.
. Αντίστροφα, η πυκνότητα μπορεί να προκύψει από τη
συνάρτηση κατανομής, όπως θα δούμε και στο επόμενο παράδειγμα.
-
- Παράδειγμα 4:
Προσδιορίστε τη συνάρτηση κατανομής της τυχαίας μεταβλητής
 του παραδείγματος 1, και δώστε τη γραφική της παράσταση.
του παραδείγματος 1, και δώστε τη γραφική της παράσταση.
Η 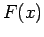 θα είναι:
θα είναι:
Για παράδειγμα, για 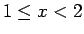 , η
, η 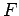 θα είναι
θα είναι
 .
Βλέπουμε ότι η
.
Βλέπουμε ότι η 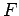 είναι μη φθίνουσα, κλιμακωτή συνάρτηση,
και ότι για κάθε ακέραιο
είναι μη φθίνουσα, κλιμακωτή συνάρτηση,
και ότι για κάθε ακέραιο 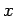 , η
, η 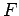 παρουσιάζει άλμα (ασυνέχεια)
μεγέθους
παρουσιάζει άλμα (ασυνέχεια)
μεγέθους 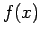 στο
στο 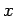 , ενώ είναι σταθερή στο διάστημα
, ενώ είναι σταθερή στο διάστημα 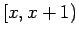 .
Έτσι, μπορούμε να προσδιορίσουμε την
.
Έτσι, μπορούμε να προσδιορίσουμε την 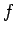 από την
από την 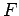 και
αντιστρόφως.
και
αντιστρόφως.
-
- Παράδειγμα 5:
Θεωρήστε τη συνάρτηση πυκνότητας
 για
για 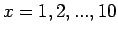 και
και 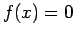 για οποιοδήποτε άλλο
για οποιοδήποτε άλλο 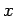 . Ποιά είναι η συνάρτηση
κατανομής
. Ποιά είναι η συνάρτηση
κατανομής 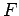 της
της 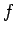 ;
;
Είναι 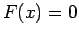 αν
αν 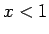 ,
, 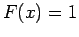 αν
αν 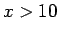 , και
, και
![$F(x) = \sum_{u \leq x} f(u) = \frac{[x]}{10}$](img81.png) , αν
, αν
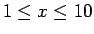 .
.
Μπορούμε να υπολογίσουμε την πιθανότητα, λόγου χάρη,
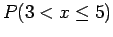 , είτε με τη βοήθεια της
, είτε με τη βοήθεια της 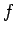 , γράφοντας
, γράφοντας
είτε με τη βοήθεια της 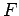 :
:
Αν θέλω να βρώ την πιθανότητα
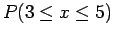 τότε γράφω
τότε γράφω
κ.τ.λ.
Γενικά, ισχύει η σχέση
η οποία είναι πολύ χρήσιμη για τον υπολογισμό πιθανοτήτων.
Maria Kafesaki
2007-06-08
![]() ως μια πραγματική μεταβλητή η οποία
για κάθε στοιχειώδες
ενδεχόμενο
ως μια πραγματική μεταβλητή η οποία
για κάθε στοιχειώδες
ενδεχόμενο ![]() του
του ![]() παίρνει μια ορισμένη τιμή (εδώ
μια από τις τιμές
-3,-1,1,3). Η πιθανότητα η
παίρνει μια ορισμένη τιμή (εδώ
μια από τις τιμές
-3,-1,1,3). Η πιθανότητα η ![]() να πάρει μια ορισμένη τιμή, έστω 1,
είναι η πιθανότητα του γεγονότος
να πάρει μια ορισμένη τιμή, έστω 1,
είναι η πιθανότητα του γεγονότος
![]() το οποίο περιλαμβάνει όλα τα στοιχειώδη
ενδεχόμενα
το οποίο περιλαμβάνει όλα τα στοιχειώδη
ενδεχόμενα ![]() του
του ![]() που οδηγούν στην τιμη
που οδηγούν στην τιμη ![]() (στο παράδειγμά μας τα ΓΓΚ, ΓΚΓ και ΚΓΓ).
Από τον πίνακα βλέπουμε ότι το
(στο παράδειγμά μας τα ΓΓΚ, ΓΚΓ και ΚΓΓ).
Από τον πίνακα βλέπουμε ότι το ![]() έχει πιθανότητα
έχει πιθανότητα
![]() να πραγματοποιηθεί (το
να πραγματοποιηθεί (το ![]() είναι η ένωση των
ανεξάρτητων ενδεχομένων ΓΓΚ, ΓΚΓ και ΚΓΓ).
Ανάλογα μπορούμε να χειριστούμε
και τις υπόλοιπες τιμές της
είναι η ένωση των
ανεξάρτητων ενδεχομένων ΓΓΚ, ΓΚΓ και ΚΓΓ).
Ανάλογα μπορούμε να χειριστούμε
και τις υπόλοιπες τιμές της ![]() . Έτσι, για κάθε τιμή που
μπορεί να πάρει η
. Έτσι, για κάθε τιμή που
μπορεί να πάρει η ![]() , έστω
, έστω ![]() (που εδώ θα είναι κάποιο από τα
(που εδώ θα είναι κάποιο από τα
![]() ), η πιθανότητα με την οποία παίρνει αυτή
την τιμή,
), η πιθανότητα με την οποία παίρνει αυτή
την τιμή, ![]() , είναι πλήρως καθορισμένη (π.χ.
, είναι πλήρως καθορισμένη (π.χ.
![]() ).
Θα δούμε ότι η
).
Θα δούμε ότι η ![]() είναι ένα παράδειγμα διακριτής τυχαίας
μεταβλητής (ή στοχαστικής συνάρτησης, όπως επίσης λέγεται).
είναι ένα παράδειγμα διακριτής τυχαίας
μεταβλητής (ή στοχαστικής συνάρτησης, όπως επίσης λέγεται).
![]() σε ένα
δειγματοχώρο
σε ένα
δειγματοχώρο ![]() είναι μια μεταβλητή
είναι μια μεταβλητή ![]() που ορίζεται για
κάθε δυνατό αποτέλεσμα ενός τυχαίου πειράματος και για κάθε τέτοιο
αποτέλεσμα παίρνει μια ορισμένη τιμή από ένα πεπερασμένο ή άπειρο
αριθμήσιμο υποσύνολο
των πραγματικών αριθμών.
που ορίζεται για
κάθε δυνατό αποτέλεσμα ενός τυχαίου πειράματος και για κάθε τέτοιο
αποτέλεσμα παίρνει μια ορισμένη τιμή από ένα πεπερασμένο ή άπειρο
αριθμήσιμο υποσύνολο
των πραγματικών αριθμών.
![]() που ορίζεται
στους πραγματικούς αριθμούς από την
που ορίζεται
στους πραγματικούς αριθμούς από την ![]() ,
λέγεται διακριτή συνάρτηση πυκνότητας ή συνάρτηση πιθανότητας
ή κατανομή πιθανότητας της
,
λέγεται διακριτή συνάρτηση πυκνότητας ή συνάρτηση πιθανότητας
ή κατανομή πιθανότητας της ![]() (Δίνει την πιθανότητα η
(Δίνει την πιθανότητα η ![]() να πάρει
μια ορισμένη τιμή από το πεδίο τιμών της.
Π.χ., για την τυχαία μεταβλητή
να πάρει
μια ορισμένη τιμή από το πεδίο τιμών της.
Π.χ., για την τυχαία μεταβλητή
![]() που ορίσαμε στην αρχή του κεφαλαίου
που ορίσαμε στην αρχή του κεφαλαίου ![]() δίνει την
πιθανότητα η
μεταβλητή
δίνει την
πιθανότητα η
μεταβλητή ![]() (το κέρδος) να πάρει την τιμή 1 (να είναι 1 ευρώ).)
(το κέρδος) να πάρει την τιμή 1 (να είναι 1 ευρώ).)
![]() που ορίσαμε στην αρχή του κεφαλαίου, και ας υποθέσουμε ότι
που ορίσαμε στην αρχή του κεφαλαίου, και ας υποθέσουμε ότι ![]() .
Τότε η
.
Τότε η ![]() έχει τη διακριτή συνάρτηση πυκνότητας που ορίζεται
από τις
έχει τη διακριτή συνάρτηση πυκνότητας που ορίζεται
από τις
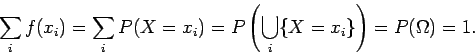
![]() ορισμένη στο
ορισμένη στο ![]() λέγεται διακριτή
συνάρτηση πυκνότητας ή απλά διακριτή πυκνότητα αν ικανοποιεί
τις παραπάνω ιδιότητες (1) - (3).
λέγεται διακριτή
συνάρτηση πυκνότητας ή απλά διακριτή πυκνότητα αν ικανοποιεί
τις παραπάνω ιδιότητες (1) - (3).
![]() δίνεται
στον παρακάτω πίνακα, μαζί με την πιθανότητα των σημείων του
δειγματοχώρου
δίνεται
στον παρακάτω πίνακα, μαζί με την πιθανότητα των σημείων του
δειγματοχώρου ![]() του πειράματος.
του πειράματος.
![]() . Με άλλα λόγια, αν μας δοθεί η
. Με άλλα λόγια, αν μας δοθεί η ![]() μπορούμε πάντα να κατασκευάσουμε ένα δειγματοχώρο
μπορούμε πάντα να κατασκευάσουμε ένα δειγματοχώρο ![]() και
μια τυχαία μεταβλητή ορισμένη στον
και
μια τυχαία μεταβλητή ορισμένη στον ![]() , της οποίας η διακριτή
πυκνότητα να είναι
, της οποίας η διακριτή
πυκνότητα να είναι ![]() . Έτσι μπορούμε να χρησιμοποιούμε
εκφράσεις όπως ``έστω
. Έτσι μπορούμε να χρησιμοποιούμε
εκφράσεις όπως ``έστω ![]() μια τυχαία μεταβλητή με διακριτή
πυκνότητα
μια τυχαία μεταβλητή με διακριτή
πυκνότητα ![]() ''
χωρίς να διευκρινίζουμε τον δειγματοχώρο
''
χωρίς να διευκρινίζουμε τον δειγματοχώρο ![]() στον οποίο ορίζεται
η
στον οποίο ορίζεται
η ![]() . Για παράδειγμα, υποθέστε ότι επιλέγουμε ένα χαρτί από μια
δεσμίδα με
. Για παράδειγμα, υποθέστε ότι επιλέγουμε ένα χαρτί από μια
δεσμίδα με ![]() χαρτιά, και θέτουμε
χαρτιά, και θέτουμε ![]() αν επιλεγεί το
αν επιλεγεί το
![]() οστο χαρτί. Τότε,
οστο χαρτί. Τότε, ![]() , άρα μπορούμε να περιγράψουμε
το πείραμα λέγοντας ότι παρατηρούμε μια τυχαία μεταβλητή
, άρα μπορούμε να περιγράψουμε
το πείραμα λέγοντας ότι παρατηρούμε μια τυχαία μεταβλητή ![]() η οποία παίρνει ακέραιες τιμές
η οποία παίρνει ακέραιες τιμές ![]() και έχει πυκνότητα
και έχει πυκνότητα
![]() αν
αν ![]() και
και ![]() αλλιώς.
αλλιώς.
![]() .
Για την ακρίβεια, το πείραμα πολλές φορές μας δίνεται ήδη μ' αυτή τη
μορφή.
.
Για την ακρίβεια, το πείραμα πολλές φορές μας δίνεται ήδη μ' αυτή τη
μορφή.
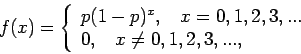
![]() είναι πυκνότητα, το μόνο που χρειάζεται
να ελέγξουμε είναι ότι ισχύει η ιδιότητα (3), αφού οι (1) και (2)
ικανοποιούνται προφανώς. Όμως,
είναι πυκνότητα, το μόνο που χρειάζεται
να ελέγξουμε είναι ότι ισχύει η ιδιότητα (3), αφού οι (1) και (2)
ικανοποιούνται προφανώς. Όμως,
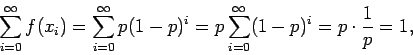
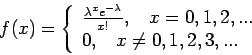
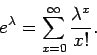
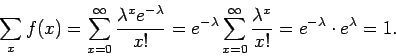
![]() ορίζεται από τη σχέση
ορίζεται από τη σχέση
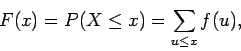
![]() θα είναι:
θα είναι:
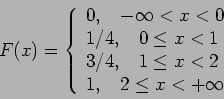
![]() αν
αν ![]() ,
, ![]() αν
αν ![]() , και
, και
![]() , αν
, αν
![]() .
.
![]() , είτε με τη βοήθεια της
, είτε με τη βοήθεια της ![]() , γράφοντας
, γράφοντας