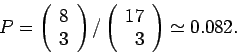Υπάρχουν περιπτώσεις (πειράματα τύχης) στις οποίες η σειρά
των στοιχείων ενός δείγματος δεν ενδιαφέρει.
Π.χ., στο πόκερ.
Ένα χέρι του πόκερ αποτελείται από 5 χαρτιά τα οποία επιλέγονται
τυχαία από μια συνηθισμένη τράπουλα με 52 χαρτιά.
Είδαμε ότι για ένα τέτοιο σύνολο υπάρχουν 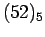 δυνατές
διατάξεις (χωρίς επανατοποθέτηση) 5 χαρτιών. Αν όμως κάνουμε
έτσι τον υπολογισμό, διαφορετικές διατάξεις των ίδιων 5 χαρτιών
θεωρούνται διαφορετικά χέρια. Όμως στο πόκερ η πεντάδα
2,3,4,5,6 σπαθιά (με αυτή τη διάταξη) είναι ίδια με την πεντάδα
3,2,4,5,6 σπαθιά (με αυτή τη διάταξη). Για την ακρίβεια, όλες
οι 5! μεταθέσεις των 5 χαρτιών είναι ισοδύναμες στο πόκερ.
Έτσι, από τα
δυνατές
διατάξεις (χωρίς επανατοποθέτηση) 5 χαρτιών. Αν όμως κάνουμε
έτσι τον υπολογισμό, διαφορετικές διατάξεις των ίδιων 5 χαρτιών
θεωρούνται διαφορετικά χέρια. Όμως στο πόκερ η πεντάδα
2,3,4,5,6 σπαθιά (με αυτή τη διάταξη) είναι ίδια με την πεντάδα
3,2,4,5,6 σπαθιά (με αυτή τη διάταξη). Για την ακρίβεια, όλες
οι 5! μεταθέσεις των 5 χαρτιών είναι ισοδύναμες στο πόκερ.
Έτσι, από τα 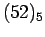 δυνατά χέρια, τα 5! από αυτά είναι απλώς
μεταθέσεις αυτών των ίδιων 5 χαρτιών.
Άρα το συνολικό πλήθος των χεριών του πόκερ, αν αγνοήσουμε τη
σειρά με την οποία εμφανίζονται τα χαρτιά, είναι
δυνατά χέρια, τα 5! από αυτά είναι απλώς
μεταθέσεις αυτών των ίδιων 5 χαρτιών.
Άρα το συνολικό πλήθος των χεριών του πόκερ, αν αγνοήσουμε τη
σειρά με την οποία εμφανίζονται τα χαρτιά, είναι 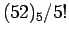 .
.
Γενικά, από ένα σύνολο 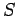 που περιέχει
που περιέχει 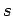 διακεκριμένα αντικείμενα,
μπορούμε να επιλέξουμε
διακεκριμένα αντικείμενα,
μπορούμε να επιλέξουμε 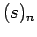 διαφορετικά δείγματα μεγέθους
διαφορετικά δείγματα μεγέθους
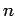 χωρίς επανατοποθέτηση. Κάθε διακεκριμένο υποσύνολο
χωρίς επανατοποθέτηση. Κάθε διακεκριμένο υποσύνολο
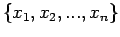 από
από 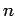 στοιχεία του
στοιχεία του 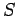 μπορεί να διαταχθεί
με
μπορεί να διαταχθεί
με 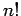 διαφορετικούς τρόπους. Αν αποφασίσουμε να αγνοήσουμε τη
σειρά με την οποία τα αντικείμενα εμφανίζονται στο δείγμα,
τότε αυτές οι
διαφορετικούς τρόπους. Αν αποφασίσουμε να αγνοήσουμε τη
σειρά με την οποία τα αντικείμενα εμφανίζονται στο δείγμα,
τότε αυτές οι 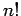 αναδιατάξεις ή μεταθέσεις πρέπει να θεωρηθούν
ταυτόσημες.
Υπάρχουν λοιπόν
αναδιατάξεις ή μεταθέσεις πρέπει να θεωρηθούν
ταυτόσημες.
Υπάρχουν λοιπόν 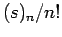 διαφορετικά δείγματα
μεγέθους
διαφορετικά δείγματα
μεγέθους 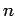 που μπορούμε να επιλέξουμε χωρίς επανατοποθέτηση
και χωρίς να μας ενδιαφέρει η διάταξη από ένα σύνολο
που μπορούμε να επιλέξουμε χωρίς επανατοποθέτηση
και χωρίς να μας ενδιαφέρει η διάταξη από ένα σύνολο 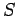 που περιέχει
που περιέχει 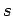 διακεκριμένα αντικείμενα. Τα δείγματα αυτά λέγονται
συνδυασμοί των
διακεκριμένα αντικείμενα. Τα δείγματα αυτά λέγονται
συνδυασμοί των 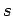 στοιχείων ανά
στοιχείων ανά 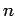 .
.
Η ποσότητα 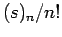 γράφεται συνήθως με τη βοήθεια του συμβόλου
του λεγόμενου διωνυμικού συντελεστή
γράφεται συνήθως με τη βοήθεια του συμβόλου
του λεγόμενου διωνυμικού συντελεστή
και μπορούμε να δούμε ότι ισούται με
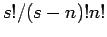
Η ορολογία "διωνυμικός συντελεστής" προέρχεται από μιά εφαρμογή
της άλγεβρας, και συγκεκριμένα το ανάπτυγμα του διωνύμου,
όπου το πλήθος των συνδυασμών
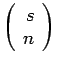 εμφανίζεται στους συντελεστές του αναπτύγματος. Οι συντελεστές
αυτοί έχουν πολλές ενδιαφέρουσες ιδιότητες, όπως για παράδειγμα
εμφανίζεται στους συντελεστές του αναπτύγματος. Οι συντελεστές
αυτοί έχουν πολλές ενδιαφέρουσες ιδιότητες, όπως για παράδειγμα
- 1)
-
- 2)
-
- 3)
-
κ. ά.,
οι οποίες αποδεικνύονται πολύ εύκολα.
Σημειώστε ότι το σύμβολο
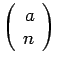 είναι καλά ορισμένο για κάθε πραγματικό αριθμό
είναι καλά ορισμένο για κάθε πραγματικό αριθμό 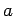 και μη αρνητικό
και μη αρνητικό 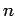 , και ότι τα
, και ότι τα 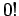 και
και 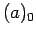 είναι
εξ ορισμού ίσα με 1.
είναι
εξ ορισμού ίσα με 1.
- Παράδειγμα 7: Πόσα είναι τα δυνατά μη διατεταγμένα
ζεύγη που μπορούμε να φτιάξουμε από τα γράμματα
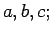
Τα ζεύγη αυτά είναι οι δυνατοί συνδυασμοί των τριών αριθμών ανά
δύο, άρα
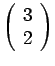
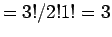 (είναι τα
(είναι τα
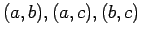 ).
).
- Παράδειγμα 8: Σύνθεση επιτροπής.
Το τμήμα Υλικών έχει 3 καθηγητές πρώτης βαθμίδας,
6 αναπληρωτές καθηγητές, και 8 επίκουρους καθηγητές.
Μια τριμέλής επιτροπή εκλέγεται τυχαία από τα παραπάνω μέλη ΔΕΠ.
Βρείτε την πιθανότητα όλα τα μέλη της επιτροπής να είναι
επίκουροι καθηγητές.
Αν ορίσουμε ως 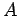 το γεγονός ``και τα τρία μέλη της επιτροπής
είναι επίκουροι'', τότε η πιθανότητα του
το γεγονός ``και τα τρία μέλη της επιτροπής
είναι επίκουροι'', τότε η πιθανότητα του 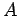 δίνεται από το πλήθος
των στοιχείων του
δίνεται από το πλήθος
των στοιχείων του 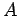 προς το συνολικό πλήθος των δειγματοσημείων του
πειράματος (που το πλήθος των δυνατών μη διατεταγμένων τριάδων που μπορούμε να
φτιάξουμε από τα υπάρχοντα μέλη ΔΕΠ).
Συνολικά, το τμήμα έχει 17 μέλη ΔΕΠ. Η επιτροπή των τριών
μπορεί να εκλεγεί από τους 17 με
προς το συνολικό πλήθος των δειγματοσημείων του
πειράματος (που το πλήθος των δυνατών μη διατεταγμένων τριάδων που μπορούμε να
φτιάξουμε από τα υπάρχοντα μέλη ΔΕΠ).
Συνολικά, το τμήμα έχει 17 μέλη ΔΕΠ. Η επιτροπή των τριών
μπορεί να εκλεγεί από τους 17 με
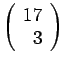 τρόπους. Υπάρχουν 8 επίκουροι καθηγητές, και οι 3 της
επιτροπής μπορούν να επιλεγούν από αυτούς με
τρόπους. Υπάρχουν 8 επίκουροι καθηγητές, και οι 3 της
επιτροπής μπορούν να επιλεγούν από αυτούς με
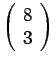 τρόπους.
τρόπους. 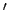 Αρα η ζητούμενη πιθανότητα είναι
Αρα η ζητούμενη πιθανότητα είναι
Σε πολλές περιπτώσεις οδηγούμαστε στον υπολογισμό παραγοντικών.
Όταν όμως ο αριθμός, έστω 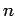 , είναι ακόμα και
μέτριου μεγέθους (για παράδειγμα
, είναι ακόμα και
μέτριου μεγέθους (για παράδειγμα 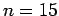 ), τότε το
), τότε το 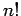 είναι πάρα πολύ μεγάλος αριθμός. Στις περιπτώσεις αυτές,
μια προσεγγιστική τιμή του
είναι πάρα πολύ μεγάλος αριθμός. Στις περιπτώσεις αυτές,
μια προσεγγιστική τιμή του 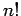 δίνεται από τον τύπο
του Stirling, σύμφωνα με τον οποίο
δίνεται από τον τύπο
του Stirling, σύμφωνα με τον οποίο
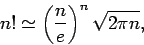
όπου 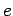 είναι η βάση των νεπέρειων λογαρίθμων (σταθερά
του Euler),
είναι η βάση των νεπέρειων λογαρίθμων (σταθερά
του Euler), 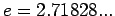 .
Μια τελευταία παρατήρηση που αφορά τον συμβολισμό:
Οι ποσότητες
.
Μια τελευταία παρατήρηση που αφορά τον συμβολισμό:
Οι ποσότητες 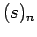 και
και 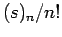 συμβολίζονται επίσης
με
συμβολίζονται επίσης
με 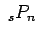 (
(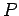 από το Permutations (μεταθέσεις) )
και
από το Permutations (μεταθέσεις) )
και 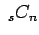 (
(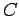 από το Combinations (συνδυασμοί) ), αντίστοιχα
από το Combinations (συνδυασμοί) ), αντίστοιχα
Maria Kafesaki
2005-05-26
![]() που περιέχει
που περιέχει ![]() διακεκριμένα αντικείμενα,
μπορούμε να επιλέξουμε
διακεκριμένα αντικείμενα,
μπορούμε να επιλέξουμε ![]() διαφορετικά δείγματα μεγέθους
διαφορετικά δείγματα μεγέθους
![]() χωρίς επανατοποθέτηση. Κάθε διακεκριμένο υποσύνολο
χωρίς επανατοποθέτηση. Κάθε διακεκριμένο υποσύνολο
![]() από
από ![]() στοιχεία του
στοιχεία του ![]() μπορεί να διαταχθεί
με
μπορεί να διαταχθεί
με ![]() διαφορετικούς τρόπους. Αν αποφασίσουμε να αγνοήσουμε τη
σειρά με την οποία τα αντικείμενα εμφανίζονται στο δείγμα,
τότε αυτές οι
διαφορετικούς τρόπους. Αν αποφασίσουμε να αγνοήσουμε τη
σειρά με την οποία τα αντικείμενα εμφανίζονται στο δείγμα,
τότε αυτές οι ![]() αναδιατάξεις ή μεταθέσεις πρέπει να θεωρηθούν
ταυτόσημες.
Υπάρχουν λοιπόν
αναδιατάξεις ή μεταθέσεις πρέπει να θεωρηθούν
ταυτόσημες.
Υπάρχουν λοιπόν ![]() διαφορετικά δείγματα
μεγέθους
διαφορετικά δείγματα
μεγέθους ![]() που μπορούμε να επιλέξουμε χωρίς επανατοποθέτηση
και χωρίς να μας ενδιαφέρει η διάταξη από ένα σύνολο
που μπορούμε να επιλέξουμε χωρίς επανατοποθέτηση
και χωρίς να μας ενδιαφέρει η διάταξη από ένα σύνολο ![]() που περιέχει
που περιέχει ![]() διακεκριμένα αντικείμενα. Τα δείγματα αυτά λέγονται
συνδυασμοί των
διακεκριμένα αντικείμενα. Τα δείγματα αυτά λέγονται
συνδυασμοί των ![]() στοιχείων ανά
στοιχείων ανά ![]() .
.
![]() γράφεται συνήθως με τη βοήθεια του συμβόλου
του λεγόμενου διωνυμικού συντελεστή
γράφεται συνήθως με τη βοήθεια του συμβόλου
του λεγόμενου διωνυμικού συντελεστή
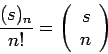
![\begin{displaymath}\left(
\begin{array}{r}
s \\
n
\end{array} \right) =
\fra...
...s (s-1)s]}
{ [1\cdot2\cdots(s-n)]n!}
= \frac{s!}{(s-n)! n!} .
\end{displaymath}](img73.png)
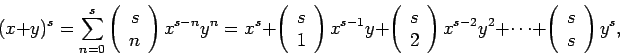
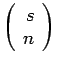 εμφανίζεται στους συντελεστές του αναπτύγματος. Οι συντελεστές
αυτοί έχουν πολλές ενδιαφέρουσες ιδιότητες, όπως για παράδειγμα
εμφανίζεται στους συντελεστές του αναπτύγματος. Οι συντελεστές
αυτοί έχουν πολλές ενδιαφέρουσες ιδιότητες, όπως για παράδειγμα
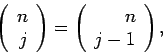
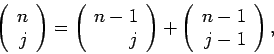
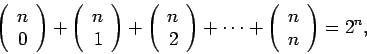
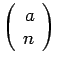 είναι καλά ορισμένο για κάθε πραγματικό αριθμό
είναι καλά ορισμένο για κάθε πραγματικό αριθμό 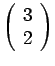
![]() (είναι τα
(είναι τα
![]() ).
).
![]() το γεγονός ``και τα τρία μέλη της επιτροπής
είναι επίκουροι'', τότε η πιθανότητα του
το γεγονός ``και τα τρία μέλη της επιτροπής
είναι επίκουροι'', τότε η πιθανότητα του ![]() δίνεται από το πλήθος
των στοιχείων του
δίνεται από το πλήθος
των στοιχείων του ![]() προς το συνολικό πλήθος των δειγματοσημείων του
πειράματος (που το πλήθος των δυνατών μη διατεταγμένων τριάδων που μπορούμε να
φτιάξουμε από τα υπάρχοντα μέλη ΔΕΠ).
Συνολικά, το τμήμα έχει 17 μέλη ΔΕΠ. Η επιτροπή των τριών
μπορεί να εκλεγεί από τους 17 με
προς το συνολικό πλήθος των δειγματοσημείων του
πειράματος (που το πλήθος των δυνατών μη διατεταγμένων τριάδων που μπορούμε να
φτιάξουμε από τα υπάρχοντα μέλη ΔΕΠ).
Συνολικά, το τμήμα έχει 17 μέλη ΔΕΠ. Η επιτροπή των τριών
μπορεί να εκλεγεί από τους 17 με
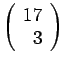 τρόπους. Υπάρχουν 8 επίκουροι καθηγητές, και οι 3 της
επιτροπής μπορούν να επιλεγούν από αυτούς με
τρόπους. Υπάρχουν 8 επίκουροι καθηγητές, και οι 3 της
επιτροπής μπορούν να επιλεγούν από αυτούς με
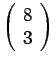 τρόπους.
τρόπους. ![]() Αρα η ζητούμενη πιθανότητα είναι
Αρα η ζητούμενη πιθανότητα είναι