Πολλά φαινόμενα έχουν την ιδιότητα η επανειλλημένη παρατήρησή
τους κάτω από συγκεκριμένες συνθήκες να οδηγεί πάντα στο ίδιο αποτέλεσμα.
Για παράδειγμα, αν αφήνουμε μια μπάλα που ήταν αρχικά
ακίνητη να πέσει από ύψος 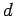 μέτρων μέσα σε έναν κύλινδρο
χωρίς αέρα, θα φτάνει στο έδαφος πάντα μετά από
μέτρων μέσα σε έναν κύλινδρο
χωρίς αέρα, θα φτάνει στο έδαφος πάντα μετά από 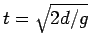 δευτερόλεπτα, όπου το
δευτερόλεπτα, όπου το 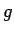 είναι η σταθερή επιτάχυνση της
βαρύτητας σε
είναι η σταθερή επιτάχυνση της
βαρύτητας σε 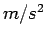 . Αυτά ανήκουν στα λεγόμενα αιτιοκρατικά φαινόμενα.
Υπάρχουν όμως άλλα φαινόμενα, των οποίων η επανειλλημένη
παρατήρηση κάτω από τις ίδιες συνθήκες δεν οδηγεί πάντα στο
ίδιο αποτέλεσμα. Λόγου χάρη, αν ρίξουμε ένα νόμισμα
1000 φορές, οι εμφανίσεις γραμμάτων (Γ) ή κεφαλής (Κ)
εναλλάσσονται με έναν φαινομενικά ακανόνιστο και απρόβλεπτο τρόπο.
Τέτοιου είδους φαινόμενα τα θεωρούμε ως τυχαία, και ένα
πείραμα όπως αυτό που μόλις περιγράφτηκε το ονομάζουμε
πείραμα τύχης (ΠΤ). Τα πειράματα τύχης (ΠΤ), ή αλλιώς τυχαία
πειράματα, είναι λοιπόν εκείνα για τα οποία η γνώση των
συνθηκών κάτω από τις οποίες εκτελούνται απλά καθορίζει ένα
σύνολο δυνατών αποτελεσμάτων για το κάθε πείραμα.
Ένα πιό απλό παράδειγμα είναι η ρίψη ενός νομίσματος.
Αν και δεν μπορούμε να προβλέψουμε το αποτέλεσμα,
γνωρίζουμε ότι θα είναι Κ ή Γ, θα ανήκει δηλαδή στο σύνολο
{Κ, Γ}.
. Αυτά ανήκουν στα λεγόμενα αιτιοκρατικά φαινόμενα.
Υπάρχουν όμως άλλα φαινόμενα, των οποίων η επανειλλημένη
παρατήρηση κάτω από τις ίδιες συνθήκες δεν οδηγεί πάντα στο
ίδιο αποτέλεσμα. Λόγου χάρη, αν ρίξουμε ένα νόμισμα
1000 φορές, οι εμφανίσεις γραμμάτων (Γ) ή κεφαλής (Κ)
εναλλάσσονται με έναν φαινομενικά ακανόνιστο και απρόβλεπτο τρόπο.
Τέτοιου είδους φαινόμενα τα θεωρούμε ως τυχαία, και ένα
πείραμα όπως αυτό που μόλις περιγράφτηκε το ονομάζουμε
πείραμα τύχης (ΠΤ). Τα πειράματα τύχης (ΠΤ), ή αλλιώς τυχαία
πειράματα, είναι λοιπόν εκείνα για τα οποία η γνώση των
συνθηκών κάτω από τις οποίες εκτελούνται απλά καθορίζει ένα
σύνολο δυνατών αποτελεσμάτων για το κάθε πείραμα.
Ένα πιό απλό παράδειγμα είναι η ρίψη ενός νομίσματος.
Αν και δεν μπορούμε να προβλέψουμε το αποτέλεσμα,
γνωρίζουμε ότι θα είναι Κ ή Γ, θα ανήκει δηλαδή στο σύνολο
{Κ, Γ}.
Παρόλο που σε πρώτη ματιά φαίνεται αδύνατο να διατυπώσουμε
αξιόλογα συμπεράσματα για τυχαία φαινόμενα,
η εμπειρία έχει δείξει ότι πολλά από τα
φαινόμενα αυτά παρουσιάζουν μια στατιστική κανονικότητα που
αξίζει να μελετηθεί. Π.χ. αν ρίξουμε ένα νόμισμα μία φορά
δεν μπορούμε να κάνουμε κάποια μη τετριμμένη πρόβλεψη για το αποτέλεσμα.
Αν ρίξουμε όμως το ίδιο νόμισμα πάρα πολλές φορές θα δούμε ότι η συχνότητα
εμφανίσης Κ και Γ είναι περίπου η ίδια και άρα το Κ εμφανίζεται περίπου
στο 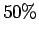 των ρίψεων.
των ρίψεων.
Άλλα απλά παραδείγματα πειραμάτων τύχης είναι
- α)
- η ρίψη ενός ζαριού,
- β)
- το τράβηγμα ενός χαρτιού από μιά συνηθισμένη
τράπουλα με 52 χαρτιά,
- γ)
- η καταγραφή της διάρκειας ζωής μιάς μπαταρίας
ή ενός ηλεκτρικού λαμπτήρα,
- δ)
- η καταγραφή των υψών των ατόμων ενός δοθέντος
πληθυσμού,
- ε)
- η επιλογή ενός βόλου από ένα δοχείο το οποίο
περιέχει
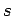 βόλους, οι οποίοι φέρουν τους αριθμούς
1,2,...,
βόλους, οι οποίοι φέρουν τους αριθμούς
1,2,...,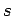 , αλλά είναι όμοιοι κατά τα άλλα,
, αλλά είναι όμοιοι κατά τα άλλα,
- στ)
- ο χρόνος διάσπασης ισοτόπου κάποιου ραδιενεργού
στοιχείου, κ.ά.
Το σύνολο όλων των δυνατών αποτελεσμάτων ενός πειράματος
τύχης λέγεται δειγματοχώρος (ΔΧ), και συμβολίζεται με 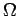 ,
και τα στοιχεία του λέγονται δειγματοσημεία ή απλά σημεία.
Έτσι, το κάθε δυνατό αποτέλεσμα ενός πειράματος τύχης
είναι ένα σημείο του
,
και τα στοιχεία του λέγονται δειγματοσημεία ή απλά σημεία.
Έτσι, το κάθε δυνατό αποτέλεσμα ενός πειράματος τύχης
είναι ένα σημείο του 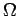 .
.
Υπάρχουν ωστόσο πολλοί τρόποι
περιγραφής των αποτελεσμάτων ενός πειράματος τύχης.
Έτσι, σε δοθέν ΠΤ αντιστοιχούν περισσότεροι του ενός
δειγματοχώροι.
-
- Παράδειγμα 1: Στο ρίξιμο του
ζαριού, ένας ΔΧ είναι ο
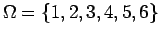 .
. 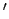 Ενας
άλλος είναι ο
Ενας
άλλος είναι ο
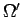 = {άρτιος, περιττός}.
= {άρτιος, περιττός}.
Στο Παράδειγμα 1, καθώς και στο παράδειγμα της ρίψης
ενός νομίσματος (όπου ο ΔΧ είναι 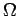 ={Κ,Γ}),
οι δειγματοχώροι έχουν πεπερασμένο πλήθος σημείων,
και λέγονται πεπερασμένοι δειγματοχώροι. Εάν τα
σημεία του δειγματοχώρου ενός τυχαίου πειράματος είναι
άπειρα, αλλά αριθμήσιμα, δηλ. μπορούν να αντιστοιχισθούν με τους φυσικούς
αριθμούς 1,2,3,4,... έναν προς έναν, τότε αυτός λέγεται
άπειρος αριθμήσιμος ΔΧ. Εάν τα άπειρα σημεία του
δειγματοχώρου δεν μπορούν να αντιστοιχισθούν με τους φυσικούς
αριθμούς 1,2,3,4,... έναν προς έναν, τότε ο ΔΧ λέγεται
άπειρος μη αριθμήσιμος.
={Κ,Γ}),
οι δειγματοχώροι έχουν πεπερασμένο πλήθος σημείων,
και λέγονται πεπερασμένοι δειγματοχώροι. Εάν τα
σημεία του δειγματοχώρου ενός τυχαίου πειράματος είναι
άπειρα, αλλά αριθμήσιμα, δηλ. μπορούν να αντιστοιχισθούν με τους φυσικούς
αριθμούς 1,2,3,4,... έναν προς έναν, τότε αυτός λέγεται
άπειρος αριθμήσιμος ΔΧ. Εάν τα άπειρα σημεία του
δειγματοχώρου δεν μπορούν να αντιστοιχισθούν με τους φυσικούς
αριθμούς 1,2,3,4,... έναν προς έναν, τότε ο ΔΧ λέγεται
άπειρος μη αριθμήσιμος.
'Ενας πεπερασμένος ή άπειρος αριθμήσιμος ΔΧ λέγεται
διακριτός ΔΧ, ενώ ένας άπειρος μη αριθμήσιμος ΔΧ λέγεται
συνεχής ΔΧ.
-
- Παράδειγμα 2: Ο χρόνος που χρειάζεται ένα ισότοπο
κάποιου ραδιενεργού στοιχείου για να διασπαστεί μπορεί να είναι
οποιοσδήποτε θετικός πραγματικός αριθμός. Στην περίπτωση αυτή,
λοιπόν, παίρνουμε ως
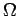 το διάστημα
το διάστημα 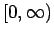 στην
πραγματική ευθεία.
στην
πραγματική ευθεία.
Maria Kafesaki
2005-05-26
![]() των ρίψεων.
των ρίψεων.
![]() ,
και τα στοιχεία του λέγονται δειγματοσημεία ή απλά σημεία.
Έτσι, το κάθε δυνατό αποτέλεσμα ενός πειράματος τύχης
είναι ένα σημείο του
,
και τα στοιχεία του λέγονται δειγματοσημεία ή απλά σημεία.
Έτσι, το κάθε δυνατό αποτέλεσμα ενός πειράματος τύχης
είναι ένα σημείο του ![]() .
.